| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 8 Introduction To Trigonometry
Welcome to the solutions for Chapter 8: Introduction to Trigonometry. This chapter opens the door to a fascinating and essential branch of mathematics that deals specifically with the relationships between the angles and the side lengths of triangles. The term "trigonometry" itself originates from Greek words meaning "triangle measurement." While trigonometry has vast applications in fields like physics, engineering, navigation, astronomy, and even music theory, this introductory chapter focuses squarely on the foundational concepts derived from right-angled triangles. We will explore how the ratios of the sides of a right triangle are uniquely determined by its acute angles, leading to the definition of the fundamental trigonometric ratios. These ratios provide a powerful way to link angles and lengths, enabling us to calculate unknown sides or angles when partial information is available. Mastering these initial concepts is crucial for further study in mathematics and science.
The cornerstone of this chapter is the definition of the six trigonometric ratios for an acute angle, let's call it $\theta$, within a right-angled triangle. These ratios relate the angle $\theta$ to the lengths of the triangle's sides: the side opposite to $\theta$ (Perpendicular, $P$), the side adjacent to $\theta$ (Base, $B$), and the side opposite the right angle (Hypotenuse, $H$). It's vital to remember that the identification of 'Perpendicular' and 'Base' is always relative to the acute angle $\theta$ being considered. The six ratios are defined as follows:
- Sine: $\sin \theta = \frac{\text{Perpendicular}}{\text{Hypotenuse}} = \frac{P}{H}$
- Cosine: $\cos \theta = \frac{\text{Base}}{\text{Hypotenuse}} = \frac{B}{H}$
- Tangent: $\tan \theta = \frac{\text{Perpendicular}}{\text{Base}} = \frac{P}{B}$
- Cosecant (reciprocal of sine): $\text{cosec } \theta = \frac{\text{Hypotenuse}}{\text{Perpendicular}} = \frac{H}{P}$
- Secant (reciprocal of cosine): $\sec \theta = \frac{\text{Hypotenuse}}{\text{Base}} = \frac{H}{B}$
- Cotangent (reciprocal of tangent): $\cot \theta = \frac{\text{Base}}{\text{Perpendicular}} = \frac{B}{P}$
Solutions demonstrate how to calculate these ratios when the side lengths are known. Conversely, if one trigonometric ratio is given, we can often find the lengths of the sides (or their proportions) using the definition and the Pythagorean theorem ($P^2 + B^2 = H^2$), subsequently allowing the calculation of the other five ratios.
A significant part of the chapter involves evaluating trigonometric ratios for specific standard angles: $0^\circ, 30^\circ, 45^\circ, 60^\circ,$ and $90^\circ$. The solutions often show how these values are derived geometrically (using equilateral and isosceles right triangles) and present them in a table for easy reference. Extensive practice is provided in substituting these standard values into various trigonometric expressions and evaluating them. Furthermore, the inherent relationships between the ratios are highlighted and utilized, such as the quotient identity $\tan \theta = \frac{\sin \theta}{\cos \theta}$ and the reciprocal identities like $\text{cosec } \theta = \frac{1}{\sin \theta}$.
The concept of complementary angles (two angles summing to $90^\circ$) leads to another set of important identities. Since the two acute angles in a right triangle are complementary, relationships emerge such as $\sin(90^\circ - \theta) = \cos \theta$, $\cos(90^\circ - \theta) = \sin \theta$, and $\tan(90^\circ - \theta) = \cot \theta$, along with corresponding identities for the reciprocal functions. The solutions demonstrate how applying these trigonometric ratios of complementary angles can simplify expressions involving angles like $18^\circ$ and $72^\circ$, or $25^\circ$ and $65^\circ$.
Finally, the chapter culminates in the introduction and proof of the three fundamental Pythagorean trigonometric identities, which are true for any angle $\theta$:
- $\sin^2\theta + \cos^2\theta = 1$
- $1 + \tan^2\theta = \sec^2\theta$
- $1 + \cot^2\theta = \text{cosec}^2\theta$
These identities are immensely important in trigonometry. The solutions extensively demonstrate their application in proving other, more complex trigonometric relationships (proving LHS = RHS) and in simplifying intricate trigonometric expressions. This chapter lays the essential groundwork for all future work involving trigonometry.
Example 1 to 5 (Before Exercise 8.1)
Example 1. Given tan A = $\frac{4}{3}$ , find the other trigonometric ratios of the angle A.
Answer:
Given
$\tan A = \frac{4}{3}$
To Find
The other trigonometric ratios of the angle A.
Solution
Consider a right-angled triangle ABC, right-angled at B, with respect to angle A.
In a right triangle, the trigonometric ratio $\tan A$ is defined as the ratio of the side opposite to angle A to the side adjacent to angle A.
$\tan A = \frac{\text{Side opposite to angle A}}{\text{Side adjacent to angle A}} = \frac{BC}{AB}$
We are given $\tan A = \frac{4}{3}$.
So, $\frac{BC}{AB} = \frac{4}{3}$.
Let $BC = 4k$ and $AB = 3k$, where $k$ is a positive constant.
By the Pythagorean theorem in $\triangle$ ABC:
$AC^2 = AB^2 + BC^2$
$AC^2 = (3k)^2 + (4k)^2$
$AC^2 = 9k^2 + 16k^2$
$AC^2 = 25k^2$
$AC = \sqrt{25k^2} = 5k$
(Since length is positive)
Now we can find the other trigonometric ratios:
$\sin A = \frac{\text{Side opposite to angle A}}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{4k}{5k} = \frac{4}{5}$
$\cos A = \frac{\text{Side adjacent to angle A}}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{3k}{5k} = \frac{3}{5}$
$\text{cosec } A = \frac{1}{\sin A} = \frac{\text{Hypotenuse}}{\text{Side opposite to angle A}} = \frac{AC}{BC} = \frac{5k}{4k} = \frac{5}{4}$
$\sec A = \frac{1}{\cos A} = \frac{\text{Hypotenuse}}{\text{Side adjacent to angle A}} = \frac{AC}{AB} = \frac{5k}{3k} = \frac{5}{3}$
$\cot A = \frac{1}{\tan A} = \frac{\text{Side adjacent to angle A}}{\text{Side opposite to angle A}} = \frac{AB}{BC} = \frac{3k}{4k} = \frac{3}{4}$
The other trigonometric ratios of angle A are:
$\sin A = \frac{4}{5}$
$\cos A = \frac{3}{5}$
$\text{cosec } A = \frac{5}{4}$
$\sec A = \frac{5}{3}$
$\cot A = \frac{3}{4}$
Example 2. If ∠B and ∠Q are acute angles such that sin B = sin Q, then prove that ∠B = ∠Q.
Answer:
Given
$\angle$B and $\angle$Q are acute angles.
$\sin B = \sin Q$.
To Prove
$\angle B = \angle Q$.
Proof
Consider two right-angled triangles, $\triangle ABC$ and $\triangle PQR$, where $\angle C = 90^\circ$ and $\angle R = 90^\circ$.
By the definition of the sine ratio:
In $\triangle ABC$, $\sin B = \frac{\text{Side opposite to }\angle B}{\text{Hypotenuse}} = \frac{AC}{AB}$
In $\triangle PQR$, $\sin Q = \frac{\text{Side opposite to }\angle Q}{\text{Hypotenuse}} = \frac{PR}{PQ}$
We are given that $\sin B = \sin Q$.
$\frac{AC}{AB} = \frac{PR}{PQ}$
…(i)
Let $\frac{AC}{AB} = \frac{PR}{PQ} = k$, where $k$ is a positive constant.
Then, $AC = k \cdot AB$ and $PR = k \cdot PQ$.
Using the Pythagorean theorem in $\triangle ABC$:
$BC^2 = AB^2 - AC^2$
$BC = \sqrt{AB^2 - AC^2} = \sqrt{AB^2 - (k \cdot AB)^2} = \sqrt{AB^2(1 - k^2)} \ $$ = AB \sqrt{1 - k^2}$
Using the Pythagorean theorem in $\triangle PQR$:
$QR^2 = PQ^2 - PR^2$
$QR = \sqrt{PQ^2 - PR^2} = \sqrt{PQ^2 - (k \cdot PQ)^2} = \sqrt{PQ^2(1 - k^2)} \ $$ = PQ \sqrt{1 - k^2}$
Now consider the ratio of the adjacent sides, BC and QR:
$\frac{BC}{QR} = \frac{AB \sqrt{1 - k^2}}{PQ \sqrt{1 - k^2}} = \frac{AB}{PQ}$
From equation (i), by rearranging the terms, we get $\frac{AC}{PR} = \frac{AB}{PQ}$.
So, we have the ratios of corresponding sides equal:
$\frac{AC}{PR} = \frac{BC}{QR} = \frac{AB}{PQ}$
Since the ratios of all three pairs of corresponding sides are equal, $\triangle ABC$ is similar to $\triangle PQR$ by the SSS similarity criterion.
$\triangle ABC \sim \triangle PQR$
(SSS similarity)
When two triangles are similar, their corresponding angles are equal.
Therefore, $\angle B = \angle Q$.
Hence Proved.
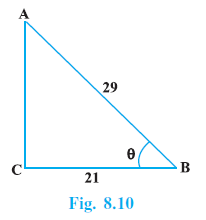
Example 3. Consider ∆ ACB, right-angled at C, in which AB = 29 units, BC = 21 units and ∠ABC = θ (see Fig. 8.10). Determine the values of
(i) cos2 θ + sin2 θ,
(ii) cos2 θ – sin2 θ.
Answer:
Given:
In $\triangle$ ACB, $\angle$C = $90^\circ$, AB = 29 units, BC = 21 units, and $\angle$ABC = $\theta$.
To Find:
(i) $\cos^2 \theta + \sin^2 \theta$
(ii) $\cos^2 \theta - \sin^2 \theta$
Solution:
In the right-angled $\triangle$ ACB, by the Pythagorean theorem, we have:
$AB^2 = AC^2 + BC^2$
$(29)^2 = AC^2 + (21)^2$
$841 = AC^2 + 441$
$AC^2 = 841 - 441$
$AC^2 = 400$
$AC = \sqrt{400} = 20$ units (Since length is positive)
Now, we determine the trigonometric ratios $\sin \theta$ and $\cos \theta$ with respect to angle $\theta$ ($\angle$ABC):
$\sin \theta = \frac{\text{Side opposite to }\theta}{\text{Hypotenuse}} = \frac{AC}{AB} = \frac{20}{29}$
$\cos \theta = \frac{\text{Side adjacent to }\theta}{\text{Hypotenuse}} = \frac{BC}{AB} = \frac{21}{29}$
(i) Value of $\cos^2 \theta + \sin^2 \theta$:
$\cos^2 \theta + \sin^2 \theta = \left(\frac{21}{29}\right)^2 + \left(\frac{20}{29}\right)^2$
$= \frac{21^2}{29^2} + \frac{20^2}{29^2}$
$= \frac{441}{841} + \frac{400}{841}$
$= \frac{441 + 400}{841}$
$= \frac{841}{841} = 1$
So, $\cos^2 \theta + \sin^2 \theta = 1$.
(ii) Value of $\cos^2 \theta - \sin^2 \theta$:
$\cos^2 \theta - \sin^2 \theta = \left(\frac{21}{29}\right)^2 - \left(\frac{20}{29}\right)^2$
$= \frac{21^2}{29^2} - \frac{20^2}{29^2}$
$= \frac{441}{841} - \frac{400}{841}$
$= \frac{441 - 400}{841}$
$= \frac{41}{841}$
So, $\cos^2 \theta - \sin^2 \theta = \frac{41}{841}$.
Example 4. In a right triangle ABC, right-angled at B, if tan A = 1, then verify that 2 sin A cos A = 1.
Answer:
Given:
In $\triangle$ ABC, $\angle$B = $90^\circ$ and $\tan A = 1$.
To Verify:
$2 \sin A \cos A = 1$.
Solution:
In a right triangle ABC, right-angled at B, the trigonometric ratio $\tan A$ is defined as the ratio of the side opposite to angle A to the side adjacent to angle A.
$\tan A = \frac{\text{Side opposite to angle A}}{\text{Side adjacent to angle A}} = \frac{BC}{AB}$
We are given $\tan A = 1$.
So, $\frac{BC}{AB} = 1$, which implies $BC = AB$.
Let $AB = BC = k$, where $k$ is a positive real number.
By the Pythagorean theorem in $\triangle$ ABC, the hypotenuse AC is:
$AC^2 = AB^2 + BC^2$
$AC^2 = k^2 + k^2$
$AC^2 = 2k^2$
$AC = \sqrt{2k^2} = k\sqrt{2}$ (Since length is positive)
Now, we find the values of $\sin A$ and $\cos A$:
$\sin A = \frac{\text{Side opposite to angle A}}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{k}{k\sqrt{2}} = \frac{1}{\sqrt{2}}$
$\cos A = \frac{\text{Side adjacent to angle A}}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{k}{k\sqrt{2}} = \frac{1}{\sqrt{2}}$
Now, we evaluate the expression $2 \sin A \cos A$:
$2 \sin A \cos A = 2 \times \left(\frac{1}{\sqrt{2}}\right) \times \left(\frac{1}{\sqrt{2}}\right)$
$= 2 \times \frac{1}{\sqrt{2} \times \sqrt{2}}$
$= 2 \times \frac{1}{2}$
$= \frac{2}{2} = 1$
$2 \sin A \cos A = 1$
Thus, we have verified that $2 \sin A \cos A = 1$ when $\tan A = 1$ in a right-angled triangle at B.
Alternate Solution:
We are given $\tan A = 1$.
We know that $\tan 45^\circ = 1$. Since A is an acute angle in a right triangle, this implies that $A = 45^\circ$.
Now, we find $\sin A$ and $\cos A$ for $A = 45^\circ$:
$\sin 45^\circ = \frac{1}{\sqrt{2}}$
$\cos 45^\circ = \frac{1}{\sqrt{2}}$
Substitute these values into the expression $2 \sin A \cos A$:
$2 \sin A \cos A = 2 \times \sin 45^\circ \times \cos 45^\circ$
$= 2 \times \frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}$
$= 2 \times \frac{1}{2}$
$= 1$
Thus, $2 \sin A \cos A = 1$ is verified.
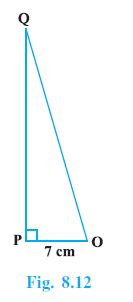
Example 5. In ∆ OPQ, right-angled at P, OP = 7 cm and OQ – PQ = 1 cm (see Fig. 8.12). Determine the values of sin Q and cos Q.
Answer:
Given:
In $\triangle$ OPQ, $\angle$P = $90^\circ$, OP = 7 cm and OQ – PQ = 1 cm.
To Find:
The values of $\sin$ Q and $\cos$ Q.
Solution:
In the right-angled $\triangle$ OPQ, we are given:
OP = 7 cm
OQ – PQ = 1 cm
... (i)
From equation (i), we can express OQ in terms of PQ:
OQ = PQ + 1
Applying the Pythagorean theorem to $\triangle$ OPQ:
$OQ^2 = OP^2 + PQ^2$
Substitute the values from the given information and the relation between OQ and PQ:
$(PQ + 1)^2 = (7)^2 + PQ^2$
Expand the left side using $(a+b)^2 = a^2 + 2ab + b^2$:
$PQ^2 + 2(PQ)(1) + 1^2 = 49 + PQ^2$
$PQ^2 + 2PQ + 1 = 49 + PQ^2$
Subtract $PQ^2$ from both sides:
$2PQ + 1 = 49$
Subtract 1 from both sides:
$2PQ = 49 - 1$
$2PQ = 48$
Divide by 2:
$PQ = \frac{48}{2}$
$PQ = 24$ cm
Now substitute the value of PQ into the relation OQ = PQ + 1:
$OQ = 24 + 1$
$OQ = 25$ cm
So, the lengths of the sides are OP = 7 cm (Opposite to angle Q), PQ = 24 cm (Adjacent to angle Q), and OQ = 25 cm (Hypotenuse).
Now, we can find the values of $\sin$ Q and $\cos$ Q:
$\sin Q = \frac{\text{Side opposite to angle Q}}{\text{Hypotenuse}} = \frac{OP}{OQ}$
$\sin Q = \frac{7}{25}$
$\cos Q = \frac{\text{Side adjacent to angle Q}}{\text{Hypotenuse}} = \frac{PQ}{OQ}$
$\cos Q = \frac{24}{25}$
The values are $\sin Q = \frac{7}{25}$ and $\cos Q = \frac{24}{25}$.
Exercise 8.1
Question 1. In ∆ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine :
(i) sin A, cos A
(ii) sin C, cos C
Answer:
Given
A right-angled triangle ∆ ABC, with the right angle at B.
Length of side AB = 24 cm.
Length of side BC = 7 cm.
To Find
(i) The values of sin A and cos A.
(ii) The values of sin C and cos C.
Solution
First, we need to find the length of the hypotenuse AC. Since ∆ ABC is a right-angled triangle, we can use the Pythagorean theorem.
According to the Pythagorean theorem:
$AC^2 = AB^2 + BC^2$
Substituting the given values:
$AC^2 = (24)^2 + (7)^2$
$AC^2 = 576 + 49$
$AC^2 = 625$
$AC = \sqrt{625}$
$AC = 25$ cm
So, the length of the hypotenuse AC is 25 cm.
(i) To determine sin A and cos A
For angle A:
The side opposite to angle A is BC = 7 cm.
The side adjacent to angle A is AB = 24 cm.
The hypotenuse is AC = 25 cm.
$\sin A = \frac{\text{Side opposite to A}}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{7}{25}$
$\cos A = \frac{\text{Side adjacent to A}}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{24}{25}$
Thus, $\sin A = \frac{7}{25}$ and $\cos A = \frac{24}{25}$.
(ii) To determine sin C and cos C
For angle C:
The side opposite to angle C is AB = 24 cm.
The side adjacent to angle C is BC = 7 cm.
The hypotenuse is AC = 25 cm.
$\sin C = \frac{\text{Side opposite to C}}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{24}{25}$
$\cos C = \frac{\text{Side adjacent to C}}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{7}{25}$
Thus, $\sin C = \frac{24}{25}$ and $\cos C = \frac{7}{25}$.
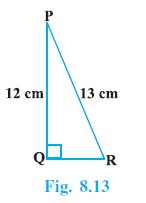
Question 2. In Fig. 8.13, find tan P – cot R.
Answer:
Given:
In $\triangle$ PQR, $\angle$Q = $90^\circ$, PQ = 12 cm, PR = 13 cm.
To Find:
$\tan$ P – $\cot$ R.
Solution:
In the right-angled $\triangle$ PQR, by the Pythagorean theorem, we have:
$PR^2 = PQ^2 + QR^2$
$(13)^2 = (12)^2 + QR^2$
$169 = 144 + QR^2$
$QR^2 = 169 - 144$
$QR^2 = 25$
$QR = \sqrt{25}$
$QR = 5$ cm (Since length must be positive)
Now, we find the values of $\tan$ P and $\cot$ R.
For angle P:
The side opposite to angle P is QR.
The side adjacent to angle P is PQ.
$\tan P = \frac{\text{Side opposite to angle P}}{\text{Side adjacent to angle P}} = \frac{QR}{PQ} = \frac{5}{12}$
For angle R:
The side opposite to angle R is PQ.
The side adjacent to angle R is QR.
$\cot R = \frac{\text{Side adjacent to angle R}}{\text{Side opposite to angle R}} = \frac{QR}{PQ} = \frac{5}{12}$
Now, we calculate $\tan$ P – $\cot$ R:
$\tan P - \cot R = \frac{5}{12} - \frac{5}{12}$
$\tan P - \cot R = 0$
Question 3. If sin A = $\frac{3}{4}$ , calculate cos A and tan A.
Answer:
Given
$\sin A = \frac{3}{4}$
To Find
The values of $\cos A$ and $\tan A$.
Solution
We are given $\sin A = \frac{3}{4}$.
In a right-angled triangle, $\sin A$ is defined as the ratio of the side opposite to angle A to the hypotenuse.
Let's consider a right triangle ABC, right-angled at B.
$\sin A = \frac{\text{Side opposite to angle A}}{\text{Hypotenuse}} = \frac{BC}{AC}$
So, $\frac{BC}{AC} = \frac{3}{4}$.
Let $BC = 3k$ and $AC = 4k$, where $k$ is a positive constant.
By the Pythagorean theorem in $\triangle$ ABC:
$AC^2 = AB^2 + BC^2$
$(4k)^2 = AB^2 + (3k)^2$
$16k^2 = AB^2 + 9k^2$
$AB^2 = 16k^2 - 9k^2$
$AB^2 = 7k^2$
$AB = \sqrt{7k^2} = k\sqrt{7}$
Now, we can find $\cos A$ and $\tan A$:
$\cos A = \frac{\text{Side adjacent to angle A}}{\text{Hypotenuse}} = \frac{AB}{AC}$
$\cos A = \frac{k\sqrt{7}}{4k} = \frac{\sqrt{7}}{4}$
$\tan A = \frac{\text{Side opposite to angle A}}{\text{Side adjacent to angle A}} = \frac{BC}{AB}$
$\tan A = \frac{3k}{k\sqrt{7}} = \frac{3}{\sqrt{7}}$
Thus, $\cos A = \frac{\sqrt{7}}{4}$ and $\tan A = \frac{3}{\sqrt{7}}$.
Question 4. Given 15 cot A = 8, find sin A and sec A.
Answer:
Given
$15 \cot A = 8$
To Find
The values of $\sin A$ and $\sec A$.
Solution
We are given the equation $15 \cot A = 8$.
Dividing both sides by 15, we get:
$\cot A = \frac{8}{15}$
In a right-angled triangle, the trigonometric ratio $\cot A$ is defined as the ratio of the side adjacent to angle A to the side opposite to angle A.
Let's consider a right triangle ABC, right-angled at B.
$\cot A = \frac{\text{Side adjacent to angle A}}{\text{Side opposite to angle A}} = \frac{AB}{BC}$
So, $\frac{AB}{BC} = \frac{8}{15}$.
Let $AB = 8k$ and $BC = 15k$, where $k$ is a positive constant.
By the Pythagorean theorem in $\triangle$ ABC:
$AC^2 = AB^2 + BC^2$
$AC^2 = (8k)^2 + (15k)^2$
$AC^2 = 64k^2 + 225k^2$
$AC^2 = 289k^2$
$AC = \sqrt{289k^2} = 17k$
Now, we can find $\sin A$ and $\sec A$:
$\sin A = \frac{\text{Side opposite to angle A}}{\text{Hypotenuse}} = \frac{BC}{AC}$
$\sin A = \frac{15k}{17k} = \frac{15}{17}$
$\sec A = \frac{\text{Hypotenuse}}{\text{Side adjacent to angle A}} = \frac{AC}{AB}$
$\sec A = \frac{17k}{8k} = \frac{17}{8}$
Thus, $\sin A = \frac{15}{17}$ and $\sec A = \frac{17}{8}$.
Question 5. Given sec θ = $\frac{13}{12}$, calculate all other trigonometric ratios.
Answer:
Given
$\sec \theta = \frac{13}{12}$
To Find
All other trigonometric ratios for angle $\theta$.
Solution
We are given $\sec \theta = \frac{13}{12}$.
In a right-angled triangle, $\sec \theta$ is defined as the ratio of the hypotenuse to the side adjacent to angle $\theta$.
Let's consider a right triangle ABC, right-angled at B, with $\angle A = \theta$.
$\sec \theta = \frac{\text{Hypotenuse}}{\text{Side adjacent to angle }\theta} = \frac{AC}{AB}$
So, $\frac{AC}{AB} = \frac{13}{12}$.
Let $AC = 13k$ and $AB = 12k$, where $k$ is a positive constant.
By the Pythagorean theorem in $\triangle$ ABC:
$AC^2 = AB^2 + BC^2$
$(13k)^2 = (12k)^2 + BC^2$
$169k^2 = 144k^2 + BC^2$
$BC^2 = 169k^2 - 144k^2$
$BC^2 = 25k^2$
$BC = \sqrt{25k^2} = 5k$
Now, we can find the other trigonometric ratios:
$\sin \theta = \frac{\text{Side opposite to angle }\theta}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{5k}{13k} = \frac{5}{13}$
$\cos \theta = \frac{\text{Side adjacent to angle }\theta}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{12k}{13k} = \frac{12}{13}$
$\tan \theta = \frac{\text{Side opposite to angle }\theta}{\text{Side adjacent to angle }\theta} = \frac{BC}{AB} = \frac{5k}{12k} = \frac{5}{12}$
$\text{cosec } \theta = \frac{\text{Hypotenuse}}{\text{Side opposite to angle }\theta} = \frac{AC}{BC} = \frac{13k}{5k} = \frac{13}{5}$
$\cot \theta = \frac{\text{Side adjacent to angle }\theta}{\text{Side opposite to angle }\theta} = \frac{AB}{BC} = \frac{12k}{5k} = \frac{12}{5}$
The other trigonometric ratios are:
$\sin \theta = \frac{5}{13}$, $\cos \theta = \frac{12}{13}$, $\tan \theta = \frac{5}{12}$, $\text{cosec } \theta = \frac{13}{5}$, $\cot \theta = \frac{12}{5}$
Question 6. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Answer:
Given
$\angle$A and $\angle$B are acute angles.
$\cos A = \cos B$.
To Show
$\angle A = \angle B$.
Proof
Consider a right-angled triangle ABC, where $\angle C = 90^\circ$. In this triangle, A and B are the acute angles.
By the definition of the cosine ratio:
For angle A, $\cos A = \frac{\text{Side adjacent to }\angle A}{\text{Hypotenuse}} = \frac{AC}{AB}$
For angle B, $\cos B = \frac{\text{Side adjacent to }\angle B}{\text{Hypotenuse}} = \frac{BC}{AB}$
We are given that $\cos A = \cos B$.
$\frac{AC}{AB} = \frac{BC}{AB}$
Multiplying both sides by AB, we get:
$AC = BC$
In $\triangle$ ABC, we know that angles opposite to equal sides are equal.
The angle opposite to side AC is $\angle B$.
The angle opposite to side BC is $\angle A$.
Since AC = BC, their opposite angles must be equal.
$\angle A = \angle B$
(Angles opposite to equal sides)
Hence Shown.
Alternate Proof
Let's consider two different right-angled triangles, $\triangle APQ$ and $\triangle BMN$, where $\angle P = 90^\circ$ and $\angle M = 90^\circ$.
Given $\cos A = \cos B$.
$\cos A = \frac{AP}{AQ}$ and $\cos B = \frac{BM}{BN}$
So, $\frac{AP}{AQ} = \frac{BM}{BN} = k$ (let)
This implies $AP = k \cdot AQ$ and $BM = k \cdot BN$.
By Pythagorean theorem:
$PQ = \sqrt{AQ^2 - AP^2} = \sqrt{AQ^2 - (k \cdot AQ)^2} = AQ\sqrt{1-k^2}$
$MN = \sqrt{BN^2 - BM^2} = \sqrt{BN^2 - (k \cdot BN)^2} = BN\sqrt{1-k^2}$
Now, consider the ratio $\frac{PQ}{MN}$:
$\frac{PQ}{MN} = \frac{AQ\sqrt{1-k^2}}{BN\sqrt{1-k^2}} = \frac{AQ}{BN}$
From our initial assumption, $\frac{AP}{AQ} = \frac{BM}{BN}$, which can be rearranged to $\frac{AP}{BM} = \frac{AQ}{BN}$.
Thus we have $\frac{AP}{BM} = \frac{AQ}{BN} = \frac{PQ}{MN}$.
By SSS similarity criterion, $\triangle APQ \sim \triangle BMN$.
Since the triangles are similar, their corresponding angles are equal.
Therefore, $\angle A = \angle B$.
Hence Shown.
Question 7. If cot θ = $\frac{7}{8}$ , evaluate :
(i) $\frac{(1 \;+\; sin\; θ) (1 \;-\; sin\; θ)}{(1 \;+\; cos\; θ) (1 \;-\; cos\; θ) }$
(ii) cot2 θ
Answer:
Given
$\cot \theta = \frac{7}{8}$
To Evaluate
(i) $\frac{(1 + \sin \theta)(1 - \sin \theta)}{(1 + \cos \theta)(1 - \cos \theta)}$
(ii) $\cot^2 \theta$
Solution
(i) Evaluate $\frac{(1 + \sin \theta)(1 - \sin \theta)}{(1 + \cos \theta)(1 - \cos \theta)}$:
We simplify the expression using the algebraic identity $(a+b)(a-b) = a^2 - b^2$.
Numerator: $(1 + \sin \theta)(1 - \sin \theta) = 1^2 - \sin^2 \theta = 1 - \sin^2 \theta$
Denominator: $(1 + \cos \theta)(1 - \cos \theta) = 1^2 - \cos^2 \theta = 1 - \cos^2 \theta$
The expression becomes: $\frac{1 - \sin^2 \theta}{1 - \cos^2 \theta}$
Using the Pythagorean identity $\sin^2 \theta + \cos^2 \theta = 1$, we know that $1 - \sin^2 \theta = \cos^2 \theta$ and $1 - \cos^2 \theta = \sin^2 \theta$.
Substituting these into the expression:
$\frac{\cos^2 \theta}{\sin^2 \theta} = \left(\frac{\cos \theta}{\sin \theta}\right)^2 = (\cot \theta)^2 = \cot^2 \theta$
We are given $\cot \theta = \frac{7}{8}$.
So, the value of the expression is $\left(\frac{7}{8}\right)^2 = \frac{49}{64}$.
(ii) Evaluate $\cot^2 \theta$:
We are given $\cot \theta = \frac{7}{8}$.
$\cot^2 \theta = (\cot \theta)^2 = \left(\frac{7}{8}\right)^2 = \frac{49}{64}$
The final answers are:
(i) $\frac{49}{64}$
(ii) $\frac{49}{64}$
Question 8. If 3 cot A = 4, check whether $\frac{1\;-\;tan^{2}A}{1\;+\;tan^{2}A}$ = cos2 A - sin2 A or not.
Answer:
Given
$3 \cot A = 4$
To Check
Whether the identity $\frac{1 - \tan^2 A}{1 + \tan^2 A} = \cos^2 A - \sin^2 A$ is true for the given value.
Solution
From the given equation, $3 \cot A = 4$, we get $\cot A = \frac{4}{3}$.
Since $\tan A = \frac{1}{\cot A}$, we have $\tan A = \frac{3}{4}$.
Let's construct a right-angled triangle ABC, right-angled at B.
$\cot A = \frac{\text{Adjacent}}{\text{Opposite}} = \frac{AB}{BC} = \frac{4}{3}$.
Let $AB = 4k$ and $BC = 3k$.
By the Pythagorean theorem: $AC^2 = AB^2 + BC^2 \ $$ = (4k)^2 + (3k)^2 \ $$ = 16k^2 + 9k^2 = 25k^2$.
So, $AC = \sqrt{25k^2} = 5k$.
Now, we find $\sin A$ and $\cos A$:
$\sin A = \frac{\text{Opposite}}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{3k}{5k} = \frac{3}{5}$
$\cos A = \frac{\text{Adjacent}}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{4k}{5k} = \frac{4}{5}$
Now, we evaluate the Left Hand Side (LHS) of the identity:
LHS = $\frac{1 - \tan^2 A}{1 + \tan^2 A} = \frac{1 - (3/4)^2}{1 + (3/4)^2} = \frac{1 - 9/16}{1 + 9/16} = \frac{(16-9)/16}{(16+9)/16} = \frac{7/16}{25/16} = \frac{7}{25}$
Next, we evaluate the Right Hand Side (RHS):
RHS = $\cos^2 A - \sin^2 A = \left(\frac{4}{5}\right)^2 - \left(\frac{3}{5}\right)^2 = \frac{16}{25} - \frac{9}{25} = \frac{16 - 9}{25} = \frac{7}{25}$
Since LHS = RHS = $\frac{7}{25}$, the given statement is true.
Yes, $\frac{1 - \tan^2 A}{1 + \tan^2 A} = \cos^2 A - \sin^2 A$.
Question 9. In triangle ABC, right-angled at B, if tan A = $\frac{1}{\sqrt{3}}$ find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Answer:
Given
In $\triangle$ ABC, $\angle B = 90^\circ$ and $\tan A = \frac{1}{\sqrt{3}}$.
To Find
(i) The value of $\sin A \cos C + \cos A \sin C$.
(ii) The value of $\cos A \cos C – \sin A \sin C$.
Solution
Given $\tan A = \frac{1}{\sqrt{3}}$.
In $\triangle$ ABC, $\tan A = \frac{\text{Opposite}}{\text{Adjacent}} = \frac{BC}{AB} = \frac{1}{\sqrt{3}}$.
Let $BC = k$ and $AB = k\sqrt{3}$.
By Pythagorean theorem: $AC^2 = AB^2 + BC^2 \ $$ = (k\sqrt{3})^2 + k^2 \ $$ = 3k^2 + k^2 = 4k^2$.
So, $AC = \sqrt{4k^2} = 2k$.
Now, we find the required trigonometric ratios for angles A and C:
$\sin A = \frac{BC}{AC} = \frac{k}{2k} = \frac{1}{2}$
$\cos A = \frac{AB}{AC} = \frac{k\sqrt{3}}{2k} = \frac{\sqrt{3}}{2}$
$\sin C = \frac{AB}{AC} = \frac{k\sqrt{3}}{2k} = \frac{\sqrt{3}}{2}$
$\cos C = \frac{BC}{AC} = \frac{k}{2k} = \frac{1}{2}$
(i) Evaluate $\sin A \cos C + \cos A \sin C$:
Substituting the values:
$= \left(\frac{1}{2}\right) \left(\frac{1}{2}\right) + \left(\frac{\sqrt{3}}{2}\right) \left(\frac{\sqrt{3}}{2}\right)$
$= \frac{1}{4} + \frac{3}{4} = \frac{4}{4} = 1$
(ii) Evaluate $\cos A \cos C – \sin A \sin C$:
Substituting the values:
$= \left(\frac{\sqrt{3}}{2}\right) \left(\frac{1}{2}\right) - \left(\frac{1}{2}\right) \left(\frac{\sqrt{3}}{2}\right)$
$= \frac{\sqrt{3}}{4} - \frac{\sqrt{3}}{4} = 0$
The final values are:
(i) 1
(ii) 0
Question 10. In ∆ PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Answer:
Given
In $\triangle PQR$, $\angle Q = 90^\circ$.
PQ = 5 cm.
PR + QR = 25 cm.
To Find
The values of $\sin P$, $\cos P$, and $\tan P$.
Solution
In the right-angled $\triangle PQR$, by the Pythagorean theorem:
$PR^2 = PQ^2 + QR^2$
... (i)
We are given PR + QR = 25 cm, so we can write PR = 25 – QR.
Substitute PR = 25 – QR and PQ = 5 into equation (i):
$(25 – QR)^2 = 5^2 + QR^2$
$625 - 50QR + QR^2 = 25 + QR^2$
Subtracting $QR^2$ from both sides:
$625 – 50QR = 25$
$625 – 25 = 50QR$
$600 = 50QR$
$QR = \frac{600}{50} = 12$ cm
Now, find PR:
PR = 25 – QR = 25 – 12 = 13 cm
So, we have the sides: PQ = 5 cm (Adjacent to P), QR = 12 cm (Opposite to P), and PR = 13 cm (Hypotenuse).
Now, we can determine the required trigonometric ratios for angle P:
$\sin P = \frac{\text{Opposite}}{\text{Hypotenuse}} = \frac{QR}{PR} = \frac{12}{13}$
$\cos P = \frac{\text{Adjacent}}{\text{Hypotenuse}} = \frac{PQ}{PR} = \frac{5}{13}$
$\tan P = \frac{\text{Opposite}}{\text{Adjacent}} = \frac{QR}{PQ} = \frac{12}{5}$
The required values are:
$\sin P = \frac{12}{13}$, $\cos P = \frac{5}{13}$, and $\tan P = \frac{12}{5}$.
Question 11. State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = $\frac{12}{5}$ for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = $\frac{4}{3}$ for some angle θ.
Answer:
(i) The value of tan A is always less than 1.
False.
Justification:
In a right-angled triangle, $\tan A = \frac{\text{Side opposite to angle A}}{\text{Side adjacent to angle A}}$.
The length of the side opposite to angle A can be greater than, equal to, or less than the length of the side adjacent to angle A, depending on the value of angle A.
For example, if $A = 45^\circ$, the opposite side equals the adjacent side, so $\tan 45^\circ = 1$.
If $A > 45^\circ$ (and $A < 90^\circ$), the side opposite to A is greater than the side adjacent to A, so $\tan A > 1$. For instance, $\tan 60^\circ = \sqrt{3} \approx 1.732$, which is greater than 1.
Therefore, the value of $\tan A$ is not always less than 1.
(ii) sec A = $\frac{12}{5}$ for some value of angle A.
True.
Justification:
In a right-angled triangle, $\sec A = \frac{\text{Hypotenuse}}{\text{Side adjacent to angle A}}$.
The hypotenuse is always the longest side in a right-angled triangle (except for the degenerate case of a right angle with zero area, where sides can be zero, but for an angle in a triangle, sides must be positive). Thus, the ratio of the hypotenuse to the adjacent side must be greater than 1.
Given $\sec A = \frac{12}{5} = 2.4$. Since $2.4 > 1$, this value is a valid value for $\sec A$ for some acute angle A.
We can form a right triangle with adjacent side 5 units and hypotenuse 12 units. By the Pythagorean theorem, the opposite side would be $\sqrt{12^2 - 5^2} = \sqrt{144 - 25} = \sqrt{119}$ units. Since $\sqrt{119}$ is a real positive number, such a triangle exists, and $\sec A = \frac{12}{5}$ is possible.
(iii) cos A is the abbreviation used for the cosecant of angle A.
False.
Justification:
$\cos A$ is the abbreviation used for the cosine of angle A.
The abbreviation used for the cosecant of angle A is $\text{cosec } A$ (or $\text{csc } A$).
(iv) cot A is the product of cot and A.
False.
Justification:
'cot' is part of the trigonometric ratio name 'cotangent'. $\cot A$ represents the cotangent of the angle A. It is not a product of 'cot' and the angle A. The expression $\cot A$ is a single entity representing the ratio of the adjacent side to the opposite side for the angle A in a right triangle.
(v) sin θ = $\frac{4}{3}$ for some angle θ.
False.
Justification:
In a right-angled triangle, $\sin \theta = \frac{\text{Side opposite to angle }\theta}{\text{Hypotenuse}}$.
The length of the side opposite to any angle in a right triangle is always less than or equal to the length of the hypotenuse. Therefore, the ratio $\frac{\text{Opposite}}{\text{Hypotenuse}}$ must be less than or equal to 1.
Given $\sin \theta = \frac{4}{3} \approx 1.33$. Since $1.33 > 1$, this value is not possible for $\sin \theta$ for any real angle $\theta$. The range of the sine function is $[-1, 1]$. For angles in a triangle (which are between $0^\circ$ and $180^\circ$), the value of sine is between 0 and 1 (inclusive).
Example 6 to 8 (Before Exercise 8.2)
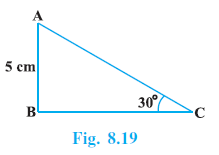
Example 6. In ∆ ABC, right-angled at B, AB = 5 cm and ∠ACB = 30° (see Fig. 8.19). Determine the lengths of the sides BC and AC.
Answer:
Given
In a right-angled triangle ∆ABC:
The right angle is at B, so $\angle B = 90^\circ$.
The length of the side AB = 5 cm.
The measure of angle ACB, $\angle C = 30^\circ$.
To Find
The lengths of the sides BC and AC.
Solution
We can use trigonometric ratios to find the lengths of the unknown sides.
With respect to the given angle $\angle C = 30^\circ$:
Side AB is the Opposite Side.
Side BC is the Adjacent Side.
Side AC is the Hypotenuse.
Finding the length of BC:
We need to find the adjacent side (BC) and we know the opposite side (AB). The trigonometric ratio that relates the opposite and adjacent sides is the tangent (tan).
$\tan C = \frac{\text{Opposite Side}}{\text{Adjacent Side}} = \frac{AB}{BC}$
Substituting the given values:
$\tan 30^\circ = \frac{5}{BC}$
We know that the value of $\tan 30^\circ = \frac{1}{\sqrt{3}}$.
$\frac{1}{\sqrt{3}} = \frac{5}{BC}$
By cross-multiplication, we get:
$BC = 5\sqrt{3}$ cm.
Finding the length of AC:
We need to find the hypotenuse (AC) and we know the opposite side (AB). The trigonometric ratio that relates the opposite side and the hypotenuse is the sine (sin).
$\sin C = \frac{\text{Opposite Side}}{\text{Hypotenuse}} = \frac{AB}{AC}$
Substituting the given values:
$\sin 30^\circ = \frac{5}{AC}$
We know that the value of $\sin 30^\circ = \frac{1}{2}$.
$\frac{1}{2} = \frac{5}{AC}$
By cross-multiplication, we get:
$AC = 5 \times 2 = 10$ cm.
Therefore, the lengths of the sides are BC = $5\sqrt{3}$ cm and AC = 10 cm.
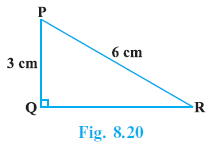
Example 7. In ∆ PQR, right-angled at Q (see Fig. 8.20), PQ = 3 cm and PR = 6 cm. Determine ∠QPR and ∠PRQ.
Answer:
Given:
In $\triangle$ PQR, $\angle$Q = $90^\circ$, PQ = 3 cm, and PR = 6 cm.
To Determine:
$\angle$QPR and $\angle$PRQ.
Solution:
In the right-angled $\triangle$ PQR, we have PQ = 3 cm and PR = 6 cm. The hypotenuse is PR.
Consider angle P ($\angle$QPR):
The side adjacent to angle P is PQ.
The hypotenuse is PR.
We can use the cosine ratio:
$\cos P = \frac{\text{Side adjacent to P}}{\text{Hypotenuse}} = \frac{PQ}{PR}$
$\cos P = \frac{3}{6} = \frac{1}{2}$
We know that $\cos 60^\circ = \frac{1}{2}$.
Since P is an acute angle in a right triangle, comparing the values, we get:
$P = 60^\circ$
So, $\angle$QPR = $60^\circ$.
Consider angle R ($\angle$PRQ):
The side opposite to angle R is PQ.
The hypotenuse is PR.
We can use the sine ratio:
$\sin R = \frac{\text{Side opposite to R}}{\text{Hypotenuse}} = \frac{PQ}{PR}$
$\sin R = \frac{3}{6} = \frac{1}{2}$
We know that $\sin 30^\circ = \frac{1}{2}$.
Since R is an acute angle in a right triangle, comparing the values, we get:
$R = 30^\circ$
So, $\angle$PRQ = $30^\circ$.
Alternatively, once we found $\angle$P = $60^\circ$, we can find $\angle$R using the angle sum property of a triangle:
In $\triangle$ PQR, $\angle$P + $\angle$Q + $\angle$R = $180^\circ$
$60^\circ + 90^\circ + \angle$R = $180^\circ$
$150^\circ + \angle$R = $180^\circ$
$\angle$R = $180^\circ - 150^\circ = 30^\circ$.
So, $\angle$PRQ = $30^\circ$.
The angles are $\angle$QPR = $60^\circ$ and $\angle$PRQ = $30^\circ$.
Example 8. If sin (A – B) = $\frac{1}{2}$ , cos (A + B) = $\frac{1}{2}$ , 0° < A + B ≤ 90°, A > B, find A and B.
Answer:
Given:
$\sin (A - B) = \frac{1}{2}$
$\cos (A + B) = \frac{1}{2}$
$0^\circ < A + B \leq 90^\circ$
$A > B$
To Find:
The values of angles A and B.
Solution:
We are given the equation $\sin (A - B) = \frac{1}{2}$.
We know that $\sin 30^\circ = \frac{1}{2}$.
Since the sine function is one-to-one for angles in the range typically considered in these problems (especially given A > B and the context of acute angles), we can equate the arguments:
A - B = $30^\circ$
... (i)
We are also given the equation $\cos (A + B) = \frac{1}{2}$.
We know that $\cos 60^\circ = \frac{1}{2}$.
The condition $0^\circ < A + B \leq 90^\circ$ tells us that A + B is an acute angle or a right angle in the first quadrant boundary. Since $\cos (A+B) = \frac{1}{2}$ (which is positive), A + B must be in the first quadrant.
Therefore, we can equate the arguments:
A + B = $60^\circ$
... (ii)
Now we have a system of two linear equations with two variables A and B:
Equation (i): $A - B = 30^\circ$
Equation (ii): $A + B = $60^\circ$
Add equation (i) and equation (ii):
$(A - B) + (A + B) = 30^\circ + 60^\circ$
$2A = 90^\circ$
$A = \frac{90^\circ}{2}$
$A = 45^\circ$
Substitute the value of A into equation (ii):
$45^\circ + B = 60^\circ$
$B = 60^\circ - 45^\circ$
$B = 15^\circ$
Let's check if these values satisfy the given conditions:
$A = 45^\circ$, $B = 15^\circ$.
$A > B$: $45^\circ > 15^\circ$ (True)
$0^\circ < A + B \leq 90^\circ$: $A + B = 45^\circ + 15^\circ = 60^\circ$. $0^\circ < 60^\circ \leq 90^\circ$ (True)
The values of A and B are $45^\circ$ and $15^\circ$ respectively.
Exercise 8.2
Question 1. Evaluate the following :
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan2 45° + cos2 30° – sin2 60°
(iii) $\frac{cos \;45°}{ sec \;30° \;+\; cosec \;30°}$
(iv) $\frac{ sin \;30° \;+\; tan \;45° \;-\; cosec \;60°}{ sec \;30° \;+\; cos\; 60° \;+\; cot\; 45°}$
(v) $\frac{5 cos^2 \;60° \;+\; 4 sec^2 \;30° \;-\; tan^2 \;45°}{sin^2 \;30° \;+\; cos^2 \;30°}$
Answer:
(i) Evaluate $\sin 60^\circ \cos 30^\circ + \sin 30^\circ \cos 60^\circ$:
We use the standard trigonometric values:
$\sin 60^\circ = \frac{\sqrt{3}}{2}$
$\cos 30^\circ = \frac{\sqrt{3}}{2}$
$\sin 30^\circ = \frac{1}{2}$
$\cos 60^\circ = \frac{1}{2}$
Substitute these values into the expression:
$\sin 60^\circ \cos 30^\circ + \sin 30^\circ \cos 60^\circ = \left(\frac{\sqrt{3}}{2}\right) \left(\frac{\sqrt{3}}{2}\right) + \left(\frac{1}{2}\right) \left(\frac{1}{2}\right)$
$= \frac{(\sqrt{3})^2}{2^2} + \frac{1^2}{2^2}$
$= \frac{3}{4} + \frac{1}{4}$
$= \frac{3 + 1}{4} = \frac{4}{4} = 1$
The value is 1.
(ii) Evaluate $2 \tan^2 45^\circ + \cos^2 30^\circ – \sin^2 60^\circ$:
We use the standard trigonometric values:
$\tan 45^\circ = 1$
$\cos 30^\circ = \frac{\sqrt{3}}{2}$
$\sin 60^\circ = \frac{\sqrt{3}}{2}$
Substitute these values into the expression:
$2 \tan^2 45^\circ + \cos^2 30^\circ – \sin^2 60^\circ = 2(1)^2 + \left(\frac{\sqrt{3}}{2}\right)^2 - \left(\frac{\sqrt{3}}{2}\right)^2$
$= 2(1) + \frac{3}{4} - \frac{3}{4}$
$= 2 + 0 = 2$
The value is 2.
(iii) Evaluate $\frac{\cos 45^\circ}{\sec 30^\circ + \text{cosec } 30^\circ}$:
We use the standard trigonometric values:
$\cos 45^\circ = \frac{1}{\sqrt{2}}$
$\sec 30^\circ = \frac{1}{\cos 30^\circ} = \frac{1}{\sqrt{3}/2} = \frac{2}{\sqrt{3}}$
$\text{cosec } 30^\circ = \frac{1}{\sin 30^\circ} = \frac{1}{1/2} = 2$
Substitute these values into the expression:
$\frac{\cos 45^\circ}{\sec 30^\circ + \text{cosec } 30^\circ} = \frac{\frac{1}{\sqrt{2}}}{\frac{2}{\sqrt{3}} + 2}$
Find a common denominator in the denominator:
$= \frac{\frac{1}{\sqrt{2}}}{\frac{2 + 2\sqrt{3}}{\sqrt{3}}}$
Invert the denominator and multiply:
$= \frac{1}{\sqrt{2}} \times \frac{\sqrt{3}}{2 + 2\sqrt{3}}$
$= \frac{\sqrt{3}}{\sqrt{2}(2 + 2\sqrt{3})}$
$= \frac{\sqrt{3}}{2\sqrt{2} + 2\sqrt{6}}$
Rationalize the denominator by multiplying the numerator and denominator by the conjugate of the denominator, which is $2\sqrt{2} - 2\sqrt{6}$ or $2(\sqrt{2} - \sqrt{6})$. It's simpler to factor out 2 first.
$= \frac{\sqrt{3}}{2(\sqrt{2} + \sqrt{6})}$
Now multiply by $\frac{\sqrt{6}-\sqrt{2}}{\sqrt{6}-\sqrt{2}}$ (conjugate of $\sqrt{2} + \sqrt{6}$ after swapping terms for easier calculation of difference of squares):
$= \frac{\sqrt{3}(\sqrt{6}-\sqrt{2})}{2(\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2})}$
$= \frac{\sqrt{18}-\sqrt{6}}{2((\sqrt{6})^2-(\sqrt{2})^2)}$
$= \frac{\sqrt{9 \times 2}-\sqrt{6}}{2(6-2)}$
$= \frac{3\sqrt{2}-\sqrt{6}}{2(4)}$
$= \frac{3\sqrt{2}-\sqrt{6}}{8}$
The value is $\frac{3\sqrt{2}-\sqrt{6}}{8}$.
(iv) Evaluate $\frac{\sin 30^\circ + \tan 45^\circ – \text{cosec } 60^\circ}{\sec 30^\circ + \cos 60^\circ + \cot 45^\circ}$:
We use the standard trigonometric values:
$\sin 30^\circ = \frac{1}{2}$
$\tan 45^\circ = 1$
$\text{cosec } 60^\circ = \frac{1}{\sin 60^\circ} = \frac{1}{\sqrt{3}/2} = \frac{2}{\sqrt{3}}$
$\sec 30^\circ = \frac{1}{\cos 30^\circ} = \frac{1}{\sqrt{3}/2} = \frac{2}{\sqrt{3}}$
$\cos 60^\circ = \frac{1}{2}$
$\cot 45^\circ = 1$
Substitute these values into the expression:
Numerator = $\sin 30^\circ + \tan 45^\circ – \text{cosec } 60^\circ = \frac{1}{2} + 1 - \frac{2}{\sqrt{3}}$
$= \frac{1}{2} + \frac{2}{2} - \frac{2}{\sqrt{3}} = \frac{3}{2} - \frac{2}{\sqrt{3}}$
Find a common denominator: $\frac{3\sqrt{3} - 4}{2\sqrt{3}}$
Denominator = $\sec 30^\circ + \cos 60^\circ + \cot 45^\circ = \frac{2}{\sqrt{3}} + \frac{1}{2} + 1$
$= \frac{2}{\sqrt{3}} + \frac{1}{2} + \frac{2}{2} = \frac{2}{\sqrt{3}} + \frac{3}{2}$
Find a common denominator: $\frac{4 + 3\sqrt{3}}{2\sqrt{3}}$
Now divide the numerator by the denominator:
$\frac{\frac{3\sqrt{3} - 4}{2\sqrt{3}}}{\frac{4 + 3\sqrt{3}}{2\sqrt{3}}} = \frac{3\sqrt{3} - 4}{2\sqrt{3}} \times \frac{2\sqrt{3}}{4 + 3\sqrt{3}}$
$= \frac{3\sqrt{3} - 4}{\cancel{2\sqrt{3}}} \times \frac{\cancel{2\sqrt{3}}}{3\sqrt{3} + 4}$
$= \frac{3\sqrt{3} - 4}{3\sqrt{3} + 4}$
Rationalize the denominator by multiplying the numerator and denominator by the conjugate of the denominator, which is $3\sqrt{3} - 4$:
$= \frac{(3\sqrt{3} - 4)(3\sqrt{3} - 4)}{(3\sqrt{3} + 4)(3\sqrt{3} - 4)}$
Use $(a-b)^2 = a^2 - 2ab + b^2$ for the numerator and $(a+b)(a-b) = a^2 - b^2$ for the denominator:
Numerator = $(3\sqrt{3})^2 - 2(3\sqrt{3})(4) + (4)^2 = (9 \times 3) - 24\sqrt{3} + 16 \ $$ = 27 - 24\sqrt{3} + 16 \ $$ = 43 - 24\sqrt{3}$
Denominator = $(3\sqrt{3})^2 - (4)^2 = (9 \times 3) - 16 = 27 - 16 = 11$
The expression is equal to $\frac{43 - 24\sqrt{3}}{11}$.
(v) Evaluate $\frac{5 \cos^2 60^\circ + 4 \sec^2 30^\circ – \tan^2 45^\circ}{\sin^2 30^\circ + \cos^2 30^\circ}$:
We use the standard trigonometric values:
$\cos 60^\circ = \frac{1}{2}$
$\sec 30^\circ = \frac{2}{\sqrt{3}}$
$\tan 45^\circ = 1$
$\sin 30^\circ = \frac{1}{2}$
$\cos 30^\circ = \frac{\sqrt{3}}{2}$
Substitute these values into the expression:
Numerator = $5 \cos^2 60^\circ + 4 \sec^2 30^\circ – \tan^2 45^\circ = 5\left(\frac{1}{2}\right)^2 + 4\left(\frac{2}{\sqrt{3}}\right)^2 - (1)^2$
$= 5\left(\frac{1}{4}\right) + 4\left(\frac{4}{3}\right) - 1$
$= \frac{5}{4} + \frac{16}{3} - 1$
Find a common denominator (12):
$= \frac{5 \times 3}{4 \times 3} + \frac{16 \times 4}{3 \times 4} - \frac{1 \times 12}{12}$
$= \frac{15}{12} + \frac{64}{12} - \frac{12}{12}$
$= \frac{15 + 64 - 12}{12} = \frac{79 - 12}{12} = \frac{67}{12}$
Denominator = $\sin^2 30^\circ + \cos^2 30^\circ = \left(\frac{1}{2}\right)^2 + \left(\frac{\sqrt{3}}{2}\right)^2$
$= \frac{1}{4} + \frac{3}{4} = \frac{1+3}{4} = \frac{4}{4} = 1$
Alternatively, using the identity $\sin^2 \theta + \cos^2 \theta = 1$, the denominator is simply 1.
Now divide the numerator by the denominator:
$\frac{\frac{67}{12}}{1} = \frac{67}{12}$
The value is $\frac{67}{12}$.
Question 2. Choose the correct option and justify your choice :
(i) $\frac{2 tan\; 30°}{1 \;+\; tan^{2}\;30°}$ =
(A) sin 60°
(B) cos 60°
(C) tan 60°
(D) sin 30°
(ii) $\frac{1 \;-\; tan^{2}\;45°}{1 \;+\; tan^{2}\;45°}$ =
(A) tan 90°
(B) 1
(C) sin 45°
(D) 0
(iii) sin 2A = 2 sin A is true when A =
(A) 0°
(B) 30°
(C) 45°
(D) 60°
(iv) $\frac{2tan \;30° }{1 \;-\; tan^{2}\;30° }$ =
(A) cos 60°
(B) sin 60°
(C) tan 60°
(D) sin 30°
Answer:
(i) $\frac{2 \tan 30^\circ}{1 + \tan^2 30^\circ}$:
We know that $\tan 30^\circ = \frac{1}{\sqrt{3}}$.
Substitute this value into the expression:
$\frac{2 (\frac{1}{\sqrt{3}})}{1 + (\frac{1}{\sqrt{3}})^2} = \frac{\frac{2}{\sqrt{3}}}{1 + \frac{1}{3}}$
$= \frac{\frac{2}{\sqrt{3}}}{\frac{3+1}{3}} = \frac{\frac{2}{\sqrt{3}}}{\frac{4}{3}}$
$= \frac{2}{\sqrt{3}} \times \frac{3}{4}$
$= \frac{\cancel{2}^1}{\sqrt{3}} \times \frac{3}{\cancel{4}^2} = \frac{3}{2\sqrt{3}}$
Rationalize the denominator:
$= \frac{3}{2\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{3\sqrt{3}}{2(3)} = \frac{\cancel{3}\sqrt{3}}{2\cancel{3}} = \frac{\sqrt{3}}{2}$
Now, we compare this value with the given options:
(A) $\sin 60^\circ = \frac{\sqrt{3}}{2}$
(B) $\cos 60^\circ = \frac{1}{2}$
(C) $\tan 60^\circ = \sqrt{3}$
(D) $\sin 30^\circ = \frac{1}{2}$
The value of the expression is equal to $\sin 60^\circ$.
The correct option is (A).
Justification: Calculation shows the expression evaluates to $\frac{\sqrt{3}}{2}$, which is the value of $\sin 60^\circ$.
(ii) $\frac{1 - \tan^2 45^\circ}{1 + \tan^2 45^\circ}$:
We know that $\tan 45^\circ = 1$.
Substitute this value into the expression:
$\frac{1 - (1)^2}{1 + (1)^2} = \frac{1 - 1}{1 + 1} = \frac{0}{2} = 0$
Now, we compare this value with the given options:
(A) $\tan 90^\circ$ (Undefined)
(B) 1
(C) $\sin 45^\circ = \frac{1}{\sqrt{2}}$
(D) 0
The value of the expression is 0.
The correct option is (D).
Justification: Calculation shows the expression evaluates to 0.
(iii) $\sin 2A = 2 \sin A$ is true when A =:
We need to check which value of A satisfies the equation $\sin 2A = 2 \sin A$.
(A) If $A = 0^\circ$:
LHS = $\sin (2 \times 0^\circ) = \sin 0^\circ = 0$
RHS = $2 \sin 0^\circ = 2 \times 0 = 0$
LHS = RHS. So, A = $0^\circ$ is a solution.
(B) If $A = 30^\circ$:
LHS = $\sin (2 \times 30^\circ) = \sin 60^\circ = \frac{\sqrt{3}}{2}$
RHS = $2 \sin 30^\circ = 2 \times \frac{1}{2} = 1$
LHS $\neq$ RHS.
(C) If $A = 45^\circ$:
LHS = $\sin (2 \times 45^\circ) = \sin 90^\circ = 1$
RHS = $2 \sin 45^\circ = 2 \times \frac{1}{\sqrt{2}} = \sqrt{2}$
LHS $\neq$ RHS.
(D) If $A = 60^\circ$:
LHS = $\sin (2 \times 60^\circ) = \sin 120^\circ$. $\sin 120^\circ \ $$ = \sin(180^\circ - 60^\circ) \ $$ = \sin 60^\circ \ $$ = \frac{\sqrt{3}}{2}$
RHS = $2 \sin 60^\circ = 2 \times \frac{\sqrt{3}}{2} = \sqrt{3}$
LHS $\neq$ RHS.
The equation $\sin 2A = 2 \sin A$ is true only when $A = 0^\circ$ (or other values not typically covered in basic trigonometry). Based on the options provided, only A = $0^\circ$ satisfies the condition.
The correct option is (A).
Justification: We checked each option and found that only A = $0^\circ$ satisfies the equation $\sin 2A = 2 \sin A$. (Using the double angle identity $\sin 2A = 2 \sin A \cos A$, the equation becomes $2 \sin A \cos A = 2 \sin A$, which simplifies to $2 \sin A \cos A - 2 \sin A = 0$, or $2 \sin A (\cos A - 1) = 0$. This is true if $\sin A = 0$ or $\cos A = 1$. Both occur when $A = 0^\circ$.)
(iv) $\frac{2 \tan 30^\circ}{1 - \tan^2 30^\circ}$:
We know that $\tan 30^\circ = \frac{1}{\sqrt{3}}$.
Substitute this value into the expression:
$\frac{2 (\frac{1}{\sqrt{3}})}{1 - (\frac{1}{\sqrt{3}})^2} = \frac{\frac{2}{\sqrt{3}}}{1 - \frac{1}{3}}$
$= \frac{\frac{2}{\sqrt{3}}}{\frac{3-1}{3}} = \frac{\frac{2}{\sqrt{3}}}{\frac{2}{3}}$
$= \frac{2}{\sqrt{3}} \times \frac{3}{2}$
$= \frac{\cancel{2}}{\sqrt{3}} \times \frac{3}{\cancel{2}} = \frac{3}{\sqrt{3}}$
Rationalize the denominator:
$= \frac{3}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{3\sqrt{3}}{3} = \sqrt{3}$
Now, we compare this value with the given options:
(A) $\cos 60^\circ = \frac{1}{2}$
(B) $\sin 60^\circ = \frac{\sqrt{3}}{2}$
(C) $\tan 60^\circ = \sqrt{3}$
(D) $\sin 30^\circ = \frac{1}{2}$
The value of the expression is equal to $\tan 60^\circ$.
The correct option is (C).
Justification: Calculation shows the expression evaluates to $\sqrt{3}$, which is the value of $\tan 60^\circ$. (This expression is also the formula for $\tan 2A$, so $\tan(2 \times 30^\circ) = \tan 60^\circ$).
Question 3. If tan (A + B) = $\sqrt{3}$ and tan (A – B) = $\frac{1}{\sqrt{3}}$ ; 0° < A + B ≤ 90°; A > B, find A and B.
Answer:
Given:
$\tan (A + B) = \sqrt{3}$
$\tan (A - B) = \frac{1}{\sqrt{3}}$
$0^\circ < A + B \leq 90^\circ$
$A > B$
To Find:
The values of angles A and B.
Solution:
We are given the equation $\tan (A + B) = \sqrt{3}$.
We know that $\tan 60^\circ = \sqrt{3}$.
Given that $0^\circ < A + B \leq 90^\circ$, and the tangent is positive, A + B must be in the first quadrant. The unique angle in this range whose tangent is $\sqrt{3}$ is $60^\circ$.
Therefore, we can equate the arguments:
A + B = $60^\circ$
... (i)
We are also given the equation $\tan (A - B) = \frac{1}{\sqrt{3}}$.
We know that $\tan 30^\circ = \frac{1}{\sqrt{3}}$.
Given that $A > B$, the difference $A - B$ must be positive. Also, since $A+B \leq 90^\circ$ and $B > 0$ (otherwise $A=A+B$ and $\tan A = \sqrt{3}$ would mean $A=60^\circ$, then $B=0$, and $\tan(60-0) = \tan 60 = \sqrt{3} \neq 1/\sqrt{3}$), it implies $A < 90^\circ$ and $B$ is also an acute angle, making $A-B$ also likely acute. The unique angle whose tangent is $\frac{1}{\sqrt{3}}$ is $30^\circ$.
Therefore, we can equate the arguments:
A - B = $30^\circ$
... (ii)
Now we have a system of two linear equations with two variables A and B:
From equation (i): $A + B = 60^\circ$
From equation (ii): $A - B = 30^\circ$
Add equation (i) and equation (ii):
$(A + B) + (A - B) = 60^\circ + 30^\circ$
$2A = 90^\circ$
$A = \frac{90^\circ}{2}$
A = $45^\circ$
Substitute the value of A = $45^\circ$ into equation (i):
$45^\circ + B = 60^\circ$
$B = 60^\circ - 45^\circ$
B = $15^\circ$
Let's verify if these values satisfy the given conditions:
$A = 45^\circ$ and $B = 15^\circ$.
$A > B$: $45^\circ > 15^\circ$. This condition is satisfied.
$0^\circ < A + B \leq 90^\circ$: $A + B = 45^\circ + 15^\circ = 60^\circ$. $0^\circ < 60^\circ \leq 90^\circ$. This condition is satisfied.
The values of A and B are $45^\circ$ and $15^\circ$ respectively.
Question 4. State whether the following are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin θ increases as θ increases.
(iii) The value of cos θ increases as θ increases.
(iv) sin θ = cos θ for all values of θ.
(v) cot A is not defined for A = 0°.
Answer:
(i) $\sin (A + B) = \sin A + \sin B$.
False.
Justification:
Consider A = $30^\circ$ and B = $60^\circ$.
LHS = $\sin (A + B) = \sin (30^\circ + 60^\circ) = \sin 90^\circ = 1$.
RHS = $\sin A + \sin B = \sin 30^\circ + \sin 60^\circ = \frac{1}{2} + \frac{\sqrt{3}}{2} = \frac{1+\sqrt{3}}{2}$.
Since $1 \neq \frac{1+\sqrt{3}}{2}$, the statement $\sin (A + B) = \sin A + \sin B$ is generally false.
(ii) The value of $\sin \theta$ increases as $\theta$ increases.
True (for $0^\circ \leq \theta \leq 90^\circ$).
Justification:
Consider the values of $\sin \theta$ for increasing $\theta$ in the range from $0^\circ$ to $90^\circ$ (which is the typical range for angles in a right triangle as considered in this chapter):
$\sin 0^\circ = 0$
$\sin 30^\circ = 0.5$
$\sin 45^\circ = \frac{1}{\sqrt{2}} \approx 0.707$
$\sin 60^\circ = \frac{\sqrt{3}}{2} \approx 0.866$
$\sin 90^\circ = 1$
As $\theta$ increases from $0^\circ$ to $90^\circ$, the value of $\sin \theta$ monotonically increases from 0 to 1. Therefore, the statement is true for this range of $\theta$.
(iii) The value of $\cos \theta$ increases as $\theta$ increases.
False.
Justification:
Consider the values of $\cos \theta$ for increasing $\theta$ in the range from $0^\circ$ to $90^\circ$:
$\cos 0^\circ = 1$
$\cos 30^\circ = \frac{\sqrt{3}}{2} \approx 0.866$
$\cos 45^\circ = \frac{1}{\sqrt{2}} \approx 0.707$
$\cos 60^\circ = 0.5$
$\cos 90^\circ = 0$
As $\theta$ increases from $0^\circ$ to $90^\circ$, the value of $\cos \theta$ monotonically decreases from 1 to 0. Therefore, the statement is false for this range of $\theta$.
(iv) $\sin \theta = \cos \theta$ for all values of $\theta$.
False.
Justification:
The equality $\sin \theta = \cos \theta$ is only true for specific values of $\theta$, such as $\theta = 45^\circ$ (or $45^\circ + n \times 180^\circ$, where $n$ is an integer). It is not true for all values of $\theta$.
For example, if $\theta = 30^\circ$, $\sin 30^\circ = \frac{1}{2}$ and $\cos 30^\circ = \frac{\sqrt{3}}{2}$. Since $\frac{1}{2} \neq \frac{\sqrt{3}}{2}$, the statement is false.
(v) $\cot A$ is not defined for $A = 0^\circ$.
True.
Justification:
The trigonometric ratio $\cot A$ is defined as $\cot A = \frac{\cos A}{\sin A}$.
For $A = 0^\circ$, we have $\cos 0^\circ = 1$ and $\sin 0^\circ = 0$.
So, $\cot 0^\circ = \frac{\cos 0^\circ}{\sin 0^\circ} = \frac{1}{0}$.
Division by zero is undefined. Therefore, $\cot A$ is not defined for $A = 0^\circ$.
Example 9 to 11 (Before Exercise 8.3)
Example 9. Evaluate $\frac{\tan 65^\circ}{\cot 25^\circ}$
Answer:
To Evaluate:
$\frac{\tan 65^\circ}{\cot 25^\circ}$
Solution:
We use the trigonometric identity for complementary angles: $\tan (90^\circ - \theta) = \cot \theta$ and $\cot (90^\circ - \theta) = \tan \theta$.
Notice that $65^\circ + 25^\circ = 90^\circ$. So, $65^\circ$ and $25^\circ$ are complementary angles.
We can write $65^\circ = 90^\circ - 25^\circ$.
So, $\tan 65^\circ = \tan (90^\circ - 25^\circ)$.
Using the identity $\tan (90^\circ - \theta) = \cot \theta$ with $\theta = 25^\circ$, we get:
$\tan 65^\circ = \cot 25^\circ$
Alternatively, we can write $25^\circ = 90^\circ - 65^\circ$.
So, $\cot 25^\circ = \cot (90^\circ - 65^\circ)$.
Using the identity $\cot (90^\circ - \theta) = \tan \theta$ with $\theta = 65^\circ$, we get:
$\cot 25^\circ = \tan 65^\circ$
Now, substitute either of these results back into the expression:
$\frac{\tan 65^\circ}{\cot 25^\circ} = \frac{\cot 25^\circ}{\cot 25^\circ} = 1$ (using $\tan 65^\circ = \cot 25^\circ$)
or
$\frac{\tan 65^\circ}{\cot 25^\circ} = \frac{\tan 65^\circ}{\tan 65^\circ} = 1$ (using $\cot 25^\circ = \tan 65^\circ$)
The value of the expression is 1.
Example 10. If sin 3A = cos (A – 26°), where 3A is an acute angle, find the value of A.
Answer:
Given:
$\sin 3A = \cos (A – 26^\circ)$
3A is an acute angle ($0^\circ < 3A < 90^\circ$).
To Find:
The value of A.
Solution:
We are given the equation $\sin 3A = \cos (A – 26^\circ)$.
We use the identity $\sin \theta = \cos (90^\circ - \theta)$.
Since 3A is an acute angle, we can write $\sin 3A$ as $\cos (90^\circ - 3A)$.
Substitute this into the given equation:
$\cos (90^\circ - 3A) = \cos (A – 26^\circ)$
Since both angles are likely acute (or within the range where cosine is one-to-one or its values correspond uniquely to acute angles in this context), we can equate the arguments:
$90^\circ - 3A = A – 26^\circ$
Rearrange the terms to solve for A:
$90^\circ + 26^\circ = A + 3A$
$116^\circ = 4A$
$A = \frac{116^\circ}{4}$
$A = 29^\circ$
Let's check if the conditions are satisfied with A = $29^\circ$:
3A = $3 \times 29^\circ = 87^\circ$. This is an acute angle ($0^\circ < 87^\circ < 90^\circ$), so the condition is satisfied.
A – $26^\circ = 29^\circ – 26^\circ = 3^\circ$. This angle is also acute and positive.
With $A = 29^\circ$, the original equation is $\sin 87^\circ = \cos 3^\circ$. This is true because $\sin 87^\circ = \sin (90^\circ - 3^\circ) = \cos 3^\circ$.
The value of A is $29^\circ$.
Example 11. Express cot 85° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Answer:
To Express:
$\cot 85^\circ + \cos 75^\circ$ in terms of trigonometric ratios of angles between $0^\circ$ and $45^\circ$.
Solution:
We need to express the given trigonometric ratios of angles $85^\circ$ and $75^\circ$ (which are greater than $45^\circ$) in terms of trigonometric ratios of angles between $0^\circ$ and $45^\circ$.
We use the complementary angle identities:
$\cot \theta = \tan (90^\circ - \theta)$
$\cos \theta = \sin (90^\circ - \theta)$
For the term $\cot 85^\circ$:
The angle is $85^\circ$. The complementary angle is $90^\circ - 85^\circ = 5^\circ$.
$\cot 85^\circ = \cot (90^\circ - 5^\circ) = \tan 5^\circ$
The angle $5^\circ$ is between $0^\circ$ and $45^\circ$.
For the term $\cos 75^\circ$:
The angle is $75^\circ$. The complementary angle is $90^\circ - 75^\circ = 15^\circ$.
$\cos 75^\circ = \cos (90^\circ - 15^\circ) = \sin 15^\circ$
The angle $15^\circ$ is between $0^\circ$ and $45^\circ$.
Now, substitute these expressions back into the original sum:
$\cot 85^\circ + \cos 75^\circ = \tan 5^\circ + \sin 15^\circ$
The expression $\cot 85^\circ + \cos 75^\circ$ is expressed in terms of trigonometric ratios of angles $5^\circ$ and $15^\circ$, both of which are between $0^\circ$ and $45^\circ$.
The expression is $\tan 5^\circ + \sin 15^\circ$.
Exercise 8.3
Question 1. Evaluate :
(i) $\frac{sin \;18°}{cos \;72°}$
(ii) $\frac{tan \;26°}{cot \;64°}$
(iii) cos 48° – sin 42°
(iv) cosec 31° – sec 59°
Answer:
(i) Evaluate $\frac{\sin 18^\circ}{\cos 72^\circ}$:
We notice that $18^\circ + 72^\circ = 90^\circ$. These are complementary angles.
We use the identity $\sin (90^\circ - \theta) = \cos \theta$ or $\cos (90^\circ - \theta) = \sin \theta$.
Let's express the numerator in terms of cosine:
$\sin 18^\circ = \sin (90^\circ - 72^\circ) = \cos 72^\circ$
Substitute this into the expression:
$\frac{\sin 18^\circ}{\cos 72^\circ} = \frac{\cos 72^\circ}{\cos 72^\circ}$
Assuming $\cos 72^\circ \neq 0$, which is true since $0^\circ < 72^\circ < 90^\circ$, we can cancel the terms.
$= 1$
Alternatively, express the denominator in terms of sine:
$\cos 72^\circ = \cos (90^\circ - 18^\circ) = \sin 18^\circ$
Substitute this into the expression:
$\frac{\sin 18^\circ}{\cos 72^\circ} = \frac{\sin 18^\circ}{\sin 18^\circ}$
Assuming $\sin 18^\circ \neq 0$, which is true since $0^\circ < 18^\circ < 90^\circ$, we can cancel the terms.
$= 1$
The value is 1.
(ii) Evaluate $\frac{\tan 26^\circ}{\cot 64^\circ}$:
We notice that $26^\circ + 64^\circ = 90^\circ$. These are complementary angles.
We use the identity $\tan (90^\circ - \theta) = \cot \theta$ or $\cot (90^\circ - \theta) = \tan \theta$.
Let's express the numerator in terms of cotangent:
$\tan 26^\circ = \tan (90^\circ - 64^\circ) = \cot 64^\circ$
Substitute this into the expression:
$\frac{\tan 26^\circ}{\cot 64^\circ} = \frac{\cot 64^\circ}{\cot 64^\circ}$
Assuming $\cot 64^\circ \neq 0$, which is true since $0^\circ < 64^\circ < 90^\circ$, we can cancel the terms.
$= 1$
The value is 1.
(iii) Evaluate $\cos 48^\circ – \sin 42^\circ$:
We notice that $48^\circ + 42^\circ = 90^\circ$. These are complementary angles.
We use the identity $\cos (90^\circ - \theta) = \sin \theta$ or $\sin (90^\circ - \theta) = \cos \theta$.
Let's express the first term in terms of sine:
$\cos 48^\circ = \cos (90^\circ - 42^\circ) = \sin 42^\circ$
Substitute this into the expression:
$\cos 48^\circ – \sin 42^\circ = \sin 42^\circ – \sin 42^\circ$
$= 0$
Alternatively, express the second term in terms of cosine:
$\sin 42^\circ = \sin (90^\circ - 48^\circ) = \cos 48^\circ$
Substitute this into the expression:
$\cos 48^\circ – \sin 42^\circ = \cos 48^\circ – \cos 48^\circ$
$= 0$
The value is 0.
(iv) Evaluate $\text{cosec } 31^\circ – \sec 59^\circ$:
We notice that $31^\circ + 59^\circ = 90^\circ$. These are complementary angles.
We use the identity $\text{cosec } (90^\circ - \theta) = \sec \theta$ or $\sec (90^\circ - \theta) = \text{cosec } \theta$.
Let's express the first term in terms of secant:
$\text{cosec } 31^\circ = \text{cosec } (90^\circ - 59^\circ) = \sec 59^\circ$
Substitute this into the expression:
$\text{cosec } 31^\circ – \sec 59^\circ = \sec 59^\circ – \sec 59^\circ$
$= 0$
Alternatively, express the second term in terms of cosecant:
$\sec 59^\circ = \sec (90^\circ - 31^\circ) = \text{cosec } 31^\circ$
Substitute this into the expression:
$\text{cosec } 31^\circ – \sec 59^\circ = \text{cosec } 31^\circ – \text{cosec } 31^\circ$
$= 0$
The value is 0.
Question 2. Show that :
(i) tan 48° tan 23° tan 42° tan 67° = 1
(ii) cos 38° cos 52° – sin 38° sin 52° = 0
Answer:
(i) Show that $\tan 48^\circ \tan 23^\circ \tan 42^\circ \tan 67^\circ = 1$:
Consider the Left Hand Side (LHS):
LHS = $\tan 48^\circ \tan 23^\circ \tan 42^\circ \tan 67^\circ$
Group the terms that are complementary:
Notice that $48^\circ + 42^\circ = 90^\circ$ and $23^\circ + 67^\circ = 90^\circ$.
We use the identity $\tan (90^\circ - \theta) = \cot \theta$.
$\tan 48^\circ = \tan (90^\circ - 42^\circ) = \cot 42^\circ$
$\tan 23^\circ = \tan (90^\circ - 67^\circ) = \cot 67^\circ$
Substitute these into the LHS:
LHS = $(\cot 42^\circ) (\cot 67^\circ) (\tan 42^\circ) (\tan 67^\circ)$
Rearrange the terms:
LHS = $(\cot 42^\circ \tan 42^\circ) (\cot 67^\circ \tan 67^\circ)$
We know that $\cot \theta \tan \theta = 1$ (since $\cot \theta = \frac{1}{\tan \theta}$).
LHS = $(1) \times (1)$
LHS = 1
This is equal to the Right Hand Side (RHS).
Hence Shown.
(ii) Show that $\cos 38^\circ \cos 52^\circ – \sin 38^\circ \sin 52^\circ = 0$:
Consider the Left Hand Side (LHS):
LHS = $\cos 38^\circ \cos 52^\circ – \sin 38^\circ \sin 52^\circ$
Notice that $38^\circ + 52^\circ = 90^\circ$. These are complementary angles.
We use the identity $\sin (90^\circ - \theta) = \cos \theta$ and $\cos (90^\circ - \theta) = \sin \theta$.
Let's express the terms involving $52^\circ$ in terms of $38^\circ$:
$\cos 52^\circ = \cos (90^\circ - 38^\circ) = \sin 38^\circ$
$\sin 52^\circ = \sin (90^\circ - 38^\circ) = \cos 38^\circ$
Substitute these into the LHS:
LHS = $\cos 38^\circ (\sin 38^\circ) – \sin 38^\circ (\cos 38^\circ)$
LHS = $\cos 38^\circ \sin 38^\circ – \sin 38^\circ \cos 38^\circ$
The two terms are identical but with opposite signs, so they cancel out.
LHS = 0
This is equal to the Right Hand Side (RHS).
Hence Shown.
Alternate Solution for (ii) (using angle sum identity):
Recall the cosine addition formula: $\cos (A + B) = \cos A \cos B - \sin A \sin B$.
The expression $\cos 38^\circ \cos 52^\circ – \sin 38^\circ \sin 52^\circ$ matches the form of $\cos (A + B)$ with $A = 38^\circ$ and $B = 52^\circ$.
LHS = $\cos (38^\circ + 52^\circ)$
LHS = $\cos 90^\circ$
We know that $\cos 90^\circ = 0$.
LHS = 0
This is equal to the RHS.
Hence Shown.
Question 3. If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.
Answer:
Given:
$\tan 2A = \cot (A – 18^\circ)$
2A is an acute angle ($0^\circ < 2A < 90^\circ$).
To Find:
The value of A.
Solution:
We are given the equation $\tan 2A = \cot (A – 18^\circ)$.
We know the trigonometric identity for complementary angles: $\tan \theta = \cot (90^\circ - \theta)$.
Since 2A is an acute angle, we can write $\tan 2A$ as $\cot (90^\circ - 2A)$.
Substitute this into the given equation:
$\cot (90^\circ - 2A) = \cot (A – 18^\circ)$
Since $2A$ is an acute angle, $90^\circ - 2A$ is also an angle between $0^\circ$ and $90^\circ$. For these angles, the cotangent function is one-to-one. Thus, we can equate the arguments of the cotangent function:
$90^\circ - 2A = A – 18^\circ$
Now, we solve this linear equation for A.
Add $2A$ to both sides:
$90^\circ = A – 18^\circ + 2A$
$90^\circ = 3A – 18^\circ$
Add $18^\circ$ to both sides:
$90^\circ + 18^\circ = 3A$
$108^\circ = 3A$
Divide by 3:
$A = \frac{108^\circ}{3}$
$A = 36^\circ$
Let's verify the condition that 2A is an acute angle:
$2A = 2 \times 36^\circ = 72^\circ$. Since $0^\circ < 72^\circ < 90^\circ$, 2A is indeed an acute angle.
Also, $A - 18^\circ = 36^\circ - 18^\circ = 18^\circ$, which is positive.
The value of A is $36^\circ$.
Question 4. If tan A = cot B, prove that A + B = 90°.
Answer:
Given:
$\tan A = \cot B$
Angles A and B are acute angles (implied by the context of trigonometric ratios in a right triangle in this section).
To Prove:
A + B = $90^\circ$.
Solution:
We are given the equation $\tan A = \cot B$.
We use the trigonometric identity for complementary angles: $\cot \theta = \tan (90^\circ - \theta)$.
We can rewrite the right side of the given equation using this identity:
$\cot B = \tan (90^\circ - B)$
Substitute this back into the given equation:
$\tan A = \tan (90^\circ - B)$
Since A and B are acute angles (and thus $90^\circ - B$ is also an angle between $0^\circ$ and $90^\circ$), and the tangent function is one-to-one for angles between $0^\circ$ and $90^\circ$, we can equate the arguments:
$A = 90^\circ - B$
Add B to both sides of the equation:
$A + B = 90^\circ$
Thus, if $\tan A = \cot B$ and A and B are acute angles, then A + B = $90^\circ$.
Hence Proved.
Alternate Solution:
We are given $\tan A = \cot B$.
We can use the identity $\tan A = \frac{\sin A}{\cos A}$ and $\cot B = \frac{\cos B}{\sin B}$.
$\frac{\sin A}{\cos A} = \frac{\cos B}{\sin B}$
Cross-multiply:
$\sin A \sin B = \cos A \cos B$
Rearrange the terms:
$\cos A \cos B - \sin A \sin B = 0$
Recognize the left side as the cosine addition formula $\cos (A + B) = \cos A \cos B - \sin A \sin B$:
$\cos (A + B) = 0$
For acute angles A and B, A + B will be in the range $(0^\circ, 180^\circ)$. The angle in this range whose cosine is 0 is $90^\circ$.
Therefore, $A + B = 90^\circ$.
Hence Proved.
Question 5. If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Answer:
Given:
$\sec 4A = \text{cosec } (A – 20^\circ)$
4A is an acute angle ($0^\circ < 4A < 90^\circ$).
To Find:
The value of A.
Solution:
We are given the equation $\sec 4A = \text{cosec } (A – 20^\circ)$.
We use the trigonometric identity for complementary angles: $\sec \theta = \text{cosec } (90^\circ - \theta)$ or $\text{cosec } \theta = \sec (90^\circ - \theta)$.
Since 4A is an acute angle, we can write $\sec 4A$ as $\text{cosec } (90^\circ - 4A)$.
Substitute this into the given equation:
$\text{cosec } (90^\circ - 4A) = \text{cosec } (A – 20^\circ)$
Since $4A$ is an acute angle, $90^\circ - 4A$ is also an angle between $0^\circ$ and $90^\circ$. For these angles, the cosecant function is one-to-one. Thus, we can equate the arguments of the cosecant function:
$90^\circ - 4A = A – 20^\circ$
Now, we solve this linear equation for A.
Add $4A$ to both sides:
$90^\circ = A – 20^\circ + 4A$
$90^\circ = 5A – 20^\circ$
Add $20^\circ$ to both sides:
$90^\circ + 20^\circ = 5A$
$110^\circ = 5A$
Divide by 5:
$A = \frac{110^\circ}{5}$
$A = 22^\circ$
Let's verify the condition that 4A is an acute angle:
$4A = 4 \times 22^\circ = 88^\circ$. Since $0^\circ < 88^\circ < 90^\circ$, 4A is indeed an acute angle.
Also, $A - 20^\circ = 22^\circ - 20^\circ = 2^\circ$, which is positive.
The value of A is $22^\circ$.
Question 6. If A, B and C are interior angles of a triangle ABC, then show that
sin $\left( \frac{B \;+\; C}{2} \right)$ = cos $\frac{A}{2}$
Answer:
Given:
A, B, and C are the interior angles of a triangle ABC.
To Show:
$\sin \left( \frac{B + C}{2} \right) = \cos \frac{A}{2}$
Solution:
Since A, B, and C are the interior angles of a triangle, their sum is $180^\circ$.
A + B + C = $180^\circ$
(Angle sum property of a triangle)
We need the expression $\frac{B+C}{2}$. Let's isolate B + C from the equation:
B + C = $180^\circ$ - A
Now, divide both sides of the equation by 2:
$\frac{B + C}{2} = \frac{180^\circ - A}{2}$
$\frac{B + C}{2} = \frac{180^\circ}{2} - \frac{A}{2}$
$\frac{B + C}{2} = 90^\circ - \frac{A}{2}$
Now, take the sine of both sides of this equation:
$\sin \left( \frac{B + C}{2} \right) = \sin \left( 90^\circ - \frac{A}{2} \right)$
We use the trigonometric identity for complementary angles: $\sin (90^\circ - \theta) = \cos \theta$.
Here, $\theta = \frac{A}{2}$.
So, $\sin \left( 90^\circ - \frac{A}{2} \right) = \cos \frac{A}{2}$.
Substitute this back into the equation:
$\sin \left( \frac{B + C}{2} \right) = \cos \frac{A}{2}$
This matches the required identity.
Hence Shown.
Question 7. Express sin 67° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Answer:
To Express:
$\sin 67^\circ + \cos 75^\circ$ in terms of trigonometric ratios of angles between $0^\circ$ and $45^\circ$.
Solution:
We need to express the given trigonometric ratios of angles $67^\circ$ and $75^\circ$ (which are greater than $45^\circ$) in terms of trigonometric ratios of angles between $0^\circ$ and $45^\circ$.
We use the complementary angle identities:
$\sin \theta = \cos (90^\circ - \theta)$
$\cos \theta = \sin (90^\circ - \theta)$
For the term $\sin 67^\circ$:
The angle is $67^\circ$. The complementary angle is $90^\circ - 67^\circ = 23^\circ$.
$\sin 67^\circ = \sin (90^\circ - 23^\circ) = \cos 23^\circ$
The angle $23^\circ$ is between $0^\circ$ and $45^\circ$.
For the term $\cos 75^\circ$:
The angle is $75^\circ$. The complementary angle is $90^\circ - 75^\circ = 15^\circ$.
$\cos 75^\circ = \cos (90^\circ - 15^\circ) = \sin 15^\circ$
The angle $15^\circ$ is between $0^\circ$ and $45^\circ$.
Now, substitute these expressions back into the original sum:
$\sin 67^\circ + \cos 75^\circ = \cos 23^\circ + \sin 15^\circ$
The expression $\sin 67^\circ + \cos 75^\circ$ is expressed in terms of trigonometric ratios of angles $23^\circ$ and $15^\circ$, both of which are between $0^\circ$ and $45^\circ$.
The expression is $\cos 23^\circ + \sin 15^\circ$.
Example 12 to 15 (Before Exercise 8.4)
Example 12. Express the ratios cos A, tan A and sec A in terms of sin A.
Answer:
Given:
Trigonometric ratios $\cos A$, $\tan A$, and $\sec A$.
To Express:
$\cos A$, $\tan A$, and $\sec A$ in terms of $\sin A$.
Solution:
We use fundamental trigonometric identities.
Expressing $\cos A$ in terms of $\sin A$:
We use the Pythagorean identity: $\sin^2 A + \cos^2 A = 1$.
Subtract $\sin^2 A$ from both sides:
$\cos^2 A = 1 - \sin^2 A$
Take the square root of both sides:
$\cos A = \pm \sqrt{1 - \sin^2 A}$
In problems involving angles in a right triangle, A is typically an acute angle ($0^\circ < A < 90^\circ$). In this range, $\cos A$ is positive. If A could be other angles, the sign would depend on the quadrant of A.
Assuming A is an acute angle:
$\cos A = \sqrt{1 - \sin^2 A}$
Expressing $\tan A$ in terms of $\sin A$:
We use the definition of tangent in terms of sine and cosine: $\tan A = \frac{\sin A}{\cos A}$.
Now substitute the expression for $\cos A$ in terms of $\sin A$ (assuming A is acute):
$\tan A = \frac{\sin A}{\sqrt{1 - \sin^2 A}}$
Expressing $\sec A$ in terms of $\sin A$:
We use the reciprocal identity: $\sec A = \frac{1}{\cos A}$.
Now substitute the expression for $\cos A$ in terms of $\sin A$ (assuming A is acute):
$\sec A = \frac{1}{\sqrt{1 - \sin^2 A}}$
Summary of the expressions in terms of $\sin A$ (assuming A is an acute angle):
$\cos A = \sqrt{1 - \sin^2 A}$
$\tan A = \frac{\sin A}{\sqrt{1 - \sin^2 A}}$
$\sec A = \frac{1}{\sqrt{1 - \sin^2 A}}$
Example 13. Prove that sec A (1 – sin A)(sec A + tan A) = 1.
Answer:
Given:
The identity $\sec A (1 – \sin A)(\sec A + \tan A) = 1$.
To Prove:
$\sec A (1 – \sin A)(\sec A + \tan A) = 1$
Proof:
Consider the Left Hand Side (LHS) of the identity:
LHS = $\sec A (1 – \sin A)(\sec A + \tan A)$
Express $\sec A$ and $\tan A$ in terms of $\sin A$ and $\cos A$ using the identities $\sec A = \frac{1}{\cos A}$ and $\tan A = \frac{\sin A}{\cos A}$.
Substitute these into the LHS:
LHS = $\frac{1}{\cos A} (1 – \sin A)\left(\frac{1}{\cos A} + \frac{\sin A}{\cos A}\right)$
Combine the terms within the second parenthesis:
LHS = $\frac{1}{\cos A} (1 – \sin A)\left(\frac{1 + \sin A}{\cos A}\right)$
Multiply the terms in the expression:
LHS = $\frac{1 \times (1 – \sin A) \times (1 + \sin A)}{\cos A \times \cos A}$
LHS = $\frac{(1 – \sin A)(1 + \sin A)}{\cos^2 A}$
Apply the algebraic identity $(a-b)(a+b) = a^2 - b^2$ to the numerator:
LHS = $\frac{1^2 – \sin^2 A}{\cos^2 A}$
LHS = $\frac{1 – \sin^2 A}{\cos^2 A}$
Use the fundamental trigonometric identity $\sin^2 A + \cos^2 A = 1$, which implies $1 – \sin^2 A = \cos^2 A$.
Substitute $1 – \sin^2 A$ with $\cos^2 A$ in the numerator:
LHS = $\frac{\cos^2 A}{\cos^2 A}$
Assuming $\cos^2 A \neq 0$ (which is true for values of A where $\sec A$ and $\tan A$ are defined, i.e., $A \neq 90^\circ, 270^\circ, ...$), we can cancel the $\cos^2 A$ terms:
LHS = 1
This is equal to the Right Hand Side (RHS).
LHS = RHS
Hence Proved.
Example 14. Prove that $\frac{cot \;A \;-\; cos \;A}{cot \;A \;+\; cos\; A}$ = $\frac{cosec \;A \;-\; 1}{cosec \;A \;+\; 1}$
Answer:
To Prove
$\frac{\cot A - \cos A}{\cot A + \cos A} = \frac{\text{cosec } A - 1}{\text{cosec } A + 1}$
Proof
We will start with the Left Hand Side (LHS) of the equation and simplify it to obtain the Right Hand Side (RHS).
LHS = $\frac{\cot A - \cos A}{\cot A + \cos A}$
We know the trigonometric identity $\cot A = \frac{\cos A}{\sin A}$. Substitute this into the LHS:
LHS = $\frac{\frac{\cos A}{\sin A} - \cos A}{\frac{\cos A}{\sin A} + \cos A}$
Now, take $\cos A$ as a common factor from both the numerator and the denominator:
LHS = $\frac{\cos A \left(\frac{1}{\sin A} - 1\right)}{\cos A \left(\frac{1}{\sin A} + 1\right)}$
Cancel the common term $\cos A$ from the numerator and the denominator (assuming $\cos A \neq 0$):
LHS = $\frac{\frac{1}{\sin A} - 1}{\frac{1}{\sin A} + 1}$
We also know the reciprocal identity $\text{cosec } A = \frac{1}{\sin A}$. Substitute this into the expression:
LHS = $\frac{\text{cosec } A - 1}{\text{cosec } A + 1}$
This expression is the same as the Right Hand Side (RHS).
Thus, LHS = RHS.
Hence, $\frac{\cot A - \cos A}{\cot A + \cos A} = \frac{\text{cosec } A - 1}{\text{cosec } A + 1}$.
Hence Proved.
Example 15. Prove that $\frac{sin \;θ \;-\; cos \;θ \;+\; 1}{sin \;θ \;+\; cos \;θ \;-\; 1}$ = $\frac{1}{sec \;θ \;-\; tan \;θ}$ , using the identity sec2 θ = 1 + tan2 θ.
Answer:
To Prove
$\frac{\sin \theta - \cos \theta + 1}{\sin \theta + \cos \theta - 1} = \frac{1}{\sec \theta - \tan \theta}$
Proof
We will start by simplifying the Left Hand Side (LHS) of the equation.
LHS = $\frac{\sin \theta - \cos \theta + 1}{\sin \theta + \cos \theta - 1}$
To use the identity involving $\sec \theta$ and $\tan \theta$, we should first express the LHS in terms of these ratios. We can achieve this by dividing both the numerator and the denominator by $\cos \theta$.
LHS = $\frac{\frac{\sin \theta}{\cos \theta} - \frac{\cos \theta}{\cos \theta} + \frac{1}{\cos \theta}}{\frac{\sin \theta}{\cos \theta} + \frac{\cos \theta}{\cos \theta} - \frac{1}{\cos \theta}}$
Using the identities $\tan \theta = \frac{\sin \theta}{\cos \theta}$ and $\sec \theta = \frac{1}{\cos \theta}$, we get:
LHS = $\frac{\tan \theta - 1 + \sec \theta}{\tan \theta + 1 - \sec \theta}$
We are given to use the identity $\sec^2 \theta = 1 + \tan^2 \theta$, which can be rearranged to $1 = \sec^2 \theta - \tan^2 \theta$.
Let's substitute this expression for '1' in the denominator:
LHS = $\frac{\tan \theta - 1 + \sec \theta}{(\tan \theta - \sec \theta) + (\sec^2 \theta - \tan^2 \theta)}$
Using the algebraic identity $a^2 - b^2 = (a-b)(a+b)$, we can factorize the term $(\sec^2 \theta - \tan^2 \theta)$:
LHS = $\frac{\tan \theta - 1 + \sec \theta}{(\tan \theta - \sec \theta) + (\sec \theta - \tan \theta)(\sec \theta + \tan \theta)}$
To simplify further, we can write $(\tan \theta - \sec \theta)$ as $-(\sec \theta - \tan \theta)$:
LHS = $\frac{\sec \theta + \tan \theta - 1}{-(\sec \theta - \tan \theta) + (\sec \theta - \tan \theta)(\sec \theta + \tan \theta)}$
Now, take $(\sec \theta - \tan \theta)$ as a common factor from the denominator:
LHS = $\frac{\sec \theta + \tan \theta - 1}{(\sec \theta - \tan \theta) [-1 + (\sec \theta + \tan \theta)]}$
LHS = $\frac{\sec \theta + \tan \theta - 1}{(\sec \theta - \tan \theta) (\sec \theta + \tan \theta - 1)}$
We can now cancel the common term $(\sec \theta + \tan \theta - 1)$ from the numerator and the denominator.
LHS = $\frac{1}{\sec \theta - \tan \theta}$
This is equal to the Right Hand Side (RHS) of the equation.
Thus, LHS = RHS.
Hence Proved.
Exercise 8.4
Question 1. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Answer:
Given:
Trigonometric ratios $\sin A$, $\sec A$, and $\tan A$.
To Express:
$\sin A$, $\sec A$, and $\tan A$ in terms of $\cot A$.
Solution:
We use fundamental trigonometric identities.
Expressing $\tan A$ in terms of $\cot A$:
We use the reciprocal identity: $\tan A = \frac{1}{\cot A}$.
Expressing $\sin A$ in terms of $\cot A$:
We use the identity $\text{cosec}^2 A = 1 + \cot^2 A$.
Taking the square root of both sides:
$\text{cosec } A = \pm \sqrt{1 + \cot^2 A}$
In this chapter, we usually consider acute angles, where trigonometric ratios are positive. So, assuming A is an acute angle:
$\text{cosec } A = \sqrt{1 + \cot^2 A}$
We also know the reciprocal identity $\sin A = \frac{1}{\text{cosec } A}$.
Substitute the expression for $\text{cosec } A$:
$\sin A = \frac{1}{\sqrt{1 + \cot^2 A}}$
Expressing $\sec A$ in terms of $\cot A$:
We use the identity $\sec^2 A = 1 + \tan^2 A$.
We already expressed $\tan A$ in terms of $\cot A$: $\tan A = \frac{1}{\cot A}$.
Substitute this into the identity for $\sec^2 A$:
$\sec^2 A = 1 + \left(\frac{1}{\cot A}\right)^2$
$\sec^2 A = 1 + \frac{1}{\cot^2 A}$
Find a common denominator on the right side:
$\sec^2 A = \frac{\cot^2 A + 1}{\cot^2 A}$
Taking the square root of both sides, and assuming A is acute (so $\sec A > 0$):
$\sec A = \sqrt{\frac{\cot^2 A + 1}{\cot^2 A}}$
$\sec A = \frac{\sqrt{1 + \cot^2 A}}{\sqrt{\cot^2 A}}$
$\sec A = \frac{\sqrt{1 + \cot^2 A}}{|\cot A|}$
For an acute angle A, $\cot A$ is positive, so $|\cot A| = \cot A$.
$\sec A = \frac{\sqrt{1 + \cot^2 A}}{\cot A}$
Summary of the expressions in terms of $\cot A$ (assuming A is an acute angle):
$\sin A = \frac{1}{\sqrt{1 + \cot^2 A}}$
$\sec A = \frac{\sqrt{1 + \cot^2 A}}{\cot A}$
$\tan A = \frac{1}{\cot A}$
Question 2. Write all the other trigonometric ratios of ∠ A in terms of sec A.
Answer:
Given:
Angle A.
To Express:
All other trigonometric ratios of $\angle$ A ($\sin A$, $\cos A$, $\tan A$, $\text{cosec } A$, $\cot A$) in terms of $\sec A$.
Solution:
We use fundamental trigonometric identities to express each ratio in terms of $\sec A$. We assume that A is an acute angle, which is standard in this context, unless otherwise specified. For acute angles, all trigonometric ratios are positive, allowing us to take the positive square root.
1. Express $\cos A$ in terms of $\sec A$:
We use the reciprocal identity:
$\cos A = \frac{1}{\sec A}$
2. Express $\tan A$ in terms of $\sec A$:
We use the identity $\sec^2 A = 1 + \tan^2 A$.
Rearrange the identity to solve for $\tan^2 A$:
$\tan^2 A = \sec^2 A - 1$
Take the square root of both sides. For acute angle A, $\tan A$ is positive, so we take the positive root:
$\tan A = \sqrt{\sec^2 A - 1}$
3. Express $\sin A$ in terms of $\sec A$:
We use the identity $\sin^2 A + \cos^2 A = 1$.
Rearrange the identity to solve for $\sin^2 A$:
$\sin^2 A = 1 - \cos^2 A$
Substitute the expression for $\cos A$ in terms of $\sec A$ ($\cos A = \frac{1}{\sec A}$):
$\sin^2 A = 1 - \left(\frac{1}{\sec A}\right)^2 = 1 - \frac{1}{\sec^2 A}$
Find a common denominator on the right side:
$\sin^2 A = \frac{\sec^2 A - 1}{\sec^2 A}$
Take the square root of both sides. For acute angle A, $\sin A$ is positive, so we take the positive root:
$\sin A = \sqrt{\frac{\sec^2 A - 1}{\sec^2 A}} = \frac{\sqrt{\sec^2 A - 1}}{\sqrt{\sec^2 A}} = \frac{\sqrt{\sec^2 A - 1}}{|\sec A|}$
For acute angle A, $\sec A$ is positive, so $|\sec A| = \sec A$:
$\sin A = \frac{\sqrt{\sec^2 A - 1}}{\sec A}$
4. Express $\text{cosec } A$ in terms of $\sec A$:
We use the reciprocal identity $\text{cosec } A = \frac{1}{\sin A}$.
Substitute the expression for $\sin A$ in terms of $\sec A$:
$\text{cosec } A = \frac{1}{\frac{\sqrt{\sec^2 A - 1}}{\sec A}}$
$\text{cosec } A = \frac{\sec A}{\sqrt{\sec^2 A - 1}}$
5. Express $\cot A$ in terms of $\sec A$:
We use the reciprocal identity $\cot A = \frac{1}{\tan A}$.
Substitute the expression for $\tan A$ in terms of $\sec A$ (assuming $\tan A > 0$):
$\cot A = \frac{1}{\sqrt{\sec^2 A - 1}}$
The other trigonometric ratios of $\angle$ A in terms of $\sec A$ (for acute angle A) are:
$\sin A = \frac{\sqrt{\sec^2 A - 1}}{\sec A}$
$\cos A = \frac{1}{\sec A}$
$\tan A = \sqrt{\sec^2 A - 1}$
$\text{cosec } A = \frac{\sec A}{\sqrt{\sec^2 A - 1}}$
$\cot A = \frac{1}{\sqrt{\sec^2 A - 1}}$
Question 3. Evaluate :
(i) $\frac{sin^2 \;63° \;+\; sin^2 \;27°}{cos^2 \;17° \;+\; cos^2 \;73°}$
(ii) sin 25° cos 65° + cos 25° sin 65°
Answer:
(i) $\frac{\sin^2 63^\circ + \sin^2 27^\circ}{\cos^2 17^\circ + \cos^2 73^\circ}$
Solution
We will use the complementary angle identities:
$\sin(90^\circ - \theta) = \cos \theta$
$\cos(90^\circ - \theta) = \sin \theta$
And the Pythagorean identity:
$\sin^2 \theta + \cos^2 \theta = 1$
First, let's simplify the numerator: $\sin^2 63^\circ + \sin^2 27^\circ$.
We can write $27^\circ$ as $(90^\circ - 63^\circ)$.
So, $\sin 27^\circ = \sin(90^\circ - 63^\circ) = \cos 63^\circ$.
Therefore, $\sin^2 27^\circ = \cos^2 63^\circ$.
The numerator becomes: $\sin^2 63^\circ + \cos^2 63^\circ$.
Using the Pythagorean identity, $\sin^2 63^\circ + \cos^2 63^\circ = 1$.
Next, let's simplify the denominator: $\cos^2 17^\circ + \cos^2 73^\circ$.
We can write $73^\circ$ as $(90^\circ - 17^\circ)$.
So, $\cos 73^\circ = \cos(90^\circ - 17^\circ) = \sin 17^\circ$.
Therefore, $\cos^2 73^\circ = \sin^2 17^\circ$.
The denominator becomes: $\cos^2 17^\circ + \sin^2 17^\circ$.
Using the Pythagorean identity, $\cos^2 17^\circ + \sin^2 17^\circ = 1$.
Now, we can evaluate the original expression:
$\frac{\sin^2 63^\circ + \sin^2 27^\circ}{\cos^2 17^\circ + \cos^2 73^\circ} = \frac{1}{1} = 1$
Thus, the value of the expression is 1.
(ii) $\sin 25^\circ \cos 65^\circ + \cos 25^\circ \sin 65^\circ$
Solution
We will use the complementary angle identities:
$\cos(90^\circ - \theta) = \sin \theta$
$\sin(90^\circ - \theta) = \cos \theta$
The expression is: $\sin 25^\circ \cos 65^\circ + \cos 25^\circ \sin 65^\circ$.
We can write the angles involving $65^\circ$ in terms of $25^\circ$, since $25^\circ + 65^\circ = 90^\circ$.
$65^\circ = 90^\circ - 25^\circ$.
So, $\cos 65^\circ = \cos(90^\circ - 25^\circ) = \sin 25^\circ$.
And, $\sin 65^\circ = \sin(90^\circ - 25^\circ) = \cos 25^\circ$.
Now, substitute these values back into the original expression:
$\sin 25^\circ (\sin 25^\circ) + \cos 25^\circ (\cos 25^\circ)$
This simplifies to:
$\sin^2 25^\circ + \cos^2 25^\circ$
Using the Pythagorean identity $\sin^2 \theta + \cos^2 \theta = 1$, we get:
$\sin^2 25^\circ + \cos^2 25^\circ = 1$
Thus, the value of the expression is 1.
Question 4. Choose the correct option. Justify your choice.
(i) 9 sec2 A – 9 tan2 A =
(A) 1
(B) 9
(C) 8
(D) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) =
(A) 0
(B) 1
(C) 2
(D) –1
(iii) (sec A + tan A) (1 – sin A) =
(A) sec A
(B) sin A
(C) cosec A
(D) cos A
(iv) $\frac{1 \;+\; tan^2 \;A}{1 \;+\; cot^2 \;A}$ =
(A) sec2 A
(B) –1
(C) cot2 A
(D) tan2 A
Answer:
(i) 9 sec2 A – 9 tan2 A
Justification
We have the expression $9 \sec^2 A - 9 \tan^2 A$.
Taking 9 as a common factor:
$9 (\sec^2 A - \tan^2 A)$
Using the trigonometric identity $\sec^2 A = 1 + \tan^2 A$, we can rearrange it to get $\sec^2 A - \tan^2 A = 1$.
Substituting this value into our expression:
$9 \times 1 = 9$
The correct option is (B) 9.
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
Justification
We convert the trigonometric ratios to their sine and cosine forms.
Expression = $\left(1 + \frac{\sin \theta}{\cos \theta} + \frac{1}{\cos \theta}\right) \left(1 + \frac{\cos \theta}{\sin \theta} - \frac{1}{\sin \theta}\right)$
Combine the terms in each bracket by taking the common denominator:
= $\left(\frac{\cos \theta + \sin \theta + 1}{\cos \theta}\right) \left(\frac{\sin \theta + \cos \theta - 1}{\sin \theta}\right)$
Multiply the numerators and denominators:
= $\frac{(\sin \theta + \cos \theta + 1)(\sin \theta + \cos \theta - 1)}{\sin \theta \cos \theta}$
The numerator is in the form of $(a+b)(a-b) = a^2 - b^2$, where $a = (\sin \theta + \cos \theta)$ and $b = 1$.
= $\frac{(\sin \theta + \cos \theta)^2 - 1^2}{\sin \theta \cos \theta}$
= $\frac{\sin^2 \theta + \cos^2 \theta + 2 \sin \theta \cos \theta - 1}{\sin \theta \cos \theta}$
Using the identity $\sin^2 \theta + \cos^2 \theta = 1$:
= $\frac{1 + 2 \sin \theta \cos \theta - 1}{\sin \theta \cos \theta}$
= $\frac{2 \sin \theta \cos \theta}{\sin \theta \cos \theta}$
= 2
The correct option is (C) 2.
(iii) (sec A + tan A) (1 – sin A)
Justification
We convert sec A and tan A to their sine and cosine forms.
Expression = $\left(\frac{1}{\cos A} + \frac{\sin A}{\cos A}\right) (1 - \sin A)$
= $\left(\frac{1 + \sin A}{\cos A}\right) (1 - \sin A)$
= $\frac{(1 + \sin A)(1 - \sin A)}{\cos A}$
Using the identity $(a+b)(a-b) = a^2 - b^2$ in the numerator:
= $\frac{1^2 - \sin^2 A}{\cos A}$
= $\frac{1 - \sin^2 A}{\cos A}$
Using the identity $\cos^2 A = 1 - \sin^2 A$:
= $\frac{\cos^2 A}{\cos A}$
= $\cos A$
The correct option is (D) cos A.
(iv) $\frac{1 + \tan^2 A}{1 + \cot^2 A}$
Justification
We use the trigonometric identities $1 + \tan^2 A = \sec^2 A$ and $1 + \cot^2 A = \text{cosec}^2 A$.
Expression = $\frac{\sec^2 A}{\text{cosec}^2 A}$
Now, we write sec A and cosec A in terms of sin A and cos A.
= $\frac{1/\cos^2 A}{1/\sin^2 A}$
= $\frac{1}{\cos^2 A} \times \frac{\sin^2 A}{1}$
= $\frac{\sin^2 A}{\cos^2 A}$
= $\tan^2 A$
The correct option is (D) tan2 A.
Question 5. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
(i) (cosec θ - cot θ)2 = $\frac{1 \;-\; cos \;θ}{ 1 \;+\; cos \;θ}$
(ii) $\frac{cos \;A}{1 \;+\; sin \;A}$ + $\frac{1 \;+\; sin \;A}{cos \;A}$ = 2 sec A
(iii) $\frac{tan \;θ}{1 \;-\; cot \;θ}$ + $\frac{cot \;θ}{1 \;-\; tan \;θ}$ = 1 + sec θ cosec θ
[Hint: Write the expression in terms of sin θ and cos θ]
(iv) $\frac{1 \;+\; sec \;A}{sec \;A}$ = $\frac{sin^2 \;A}{1 \;-\; cos \;A}$
[Hint: Simplify LHS and RHS separately]
(v) $\frac{cos \;A \;-\; sin \;A \;+\; 1}{cos \;A \;+\; sin \;A \;-\; 1}$ = cosec A + cot A, using the identity cosec2 A = 1 + cot2 A.
(vi) $\sqrt{\frac{1 \;+\; sin \;A}{1 \;-\; sin \;A}}$ = sec A + tan A
(vii) $\frac{sin \;θ \;-\; 2sin^3 \;θ}{2 cos^3 \;θ \;-\; cos \;θ}$ = tan θ
(viii) (sin A + cosec A)2 + (cos A + sec A)2 = 7 + tan2 A + cot2 A
(ix) (cosec A – sin A)(sec A – cos A) = $\frac{1}{tan \;A \;+\; cot \;A}$
[Hint: Simplify LHS and RHS separately]
(x) $\left( \frac{1\;+\;tan^{2}\;A}{1\;+\;cot^{2}\;A} \right)$ = $\left(\frac{1\;-\;tan \;A}{1\;-\;cot \;A} \right)^{2}$ = tan2 A
Answer:
(i) (cosec θ - cot θ)2 = $\frac{1 \;-\; cos \;θ}{ 1 \;+\; cos \;θ}$
Proof
LHS = $(\text{cosec } \theta - \cot \theta)^2$
Convert to sin and cos:
= $\left(\frac{1}{\sin \theta} - \frac{\cos \theta}{\sin \theta}\right)^2$
= $\left(\frac{1 - \cos \theta}{\sin \theta}\right)^2$
= $\frac{(1 - \cos \theta)^2}{\sin^2 \theta}$
Using the identity $\sin^2 \theta = 1 - \cos^2 \theta$:
= $\frac{(1 - \cos \theta)^2}{1 - \cos^2 \theta}$
Factoring the denominator using $a^2-b^2 = (a-b)(a+b)$:
= $\frac{(1 - \cos \theta)(1 - \cos \theta)}{(1 - \cos \theta)(1 + \cos \theta)}$
= $\frac{1 - \cos \theta}{1 + \cos \theta}$ = RHS
Hence Proved.
(ii) $\frac{cos \;A}{1 \;+\; sin \;A}$ + $\frac{1 \;+\; sin \;A}{cos \;A}$ = 2 sec A
Proof
LHS = $\frac{\cos A}{1 + \sin A} + \frac{1 + \sin A}{\cos A}$
Taking the LCM of the denominators:
= $\frac{\cos^2 A + (1 + \sin A)^2}{(1 + \sin A)\cos A}$
Expanding the numerator:
= $\frac{\cos^2 A + 1 + 2\sin A + \sin^2 A}{(1 + \sin A)\cos A}$
Using the identity $\sin^2 A + \cos^2 A = 1$:
= $\frac{( \sin^2 A + \cos^2 A) + 1 + 2\sin A}{(1 + \sin A)\cos A}$
= $\frac{1 + 1 + 2\sin A}{(1 + \sin A)\cos A} = \frac{2 + 2\sin A}{(1 + \sin A)\cos A}$
Taking 2 as a common factor in the numerator:
= $\frac{2(1 + \sin A)}{(1 + \sin A)\cos A}$
= $\frac{2}{\cos A} = 2 \sec A$ = RHS
Hence Proved.
(iii) $\frac{tan \;θ}{1 \;-\; cot \;θ}$ + $\frac{cot \;θ}{1 \;-\; tan \;θ}$ = 1 + sec θ cosec θ
Proof
LHS = $\frac{\tan \theta}{1 - \cot \theta} + \frac{\cot \theta}{1 - \tan \theta}$
Convert to sin and cos:
= $\frac{\frac{\sin \theta}{\cos \theta}}{1 - \frac{\cos \theta}{\sin \theta}} + \frac{\frac{\cos \theta}{\sin \theta}}{1 - \frac{\sin \theta}{\cos \theta}}$
= $\frac{\frac{\sin \theta}{\cos \theta}}{\frac{\sin \theta - \cos \theta}{\sin \theta}} + \frac{\frac{\cos \theta}{\sin \theta}}{\frac{\cos \theta - \sin \theta}{\cos \theta}}$
= $\frac{\sin^2 \theta}{\cos \theta (\sin \theta - \cos \theta)} + \frac{\cos^2 \theta}{\sin \theta (\cos \theta - \sin \theta)}$
= $\frac{\sin^2 \theta}{\cos \theta (\sin \theta - \cos \theta)} - \frac{\cos^2 \theta}{\sin \theta (\sin \theta - \cos \theta)}$
Taking a common denominator:
= $\frac{\sin^3 \theta - \cos^3 \theta}{\sin \theta \cos \theta (\sin \theta - \cos \theta)}$
Using the identity $a^3 - b^3 = (a-b)(a^2 + ab + b^2)$:
= $\frac{(\sin \theta - \cos \theta)(\sin^2 \theta + \sin \theta \cos \theta + \cos^2 \theta)}{\sin \theta \cos \theta (\sin \theta - \cos \theta)}$
Using the identity $\sin^2 \theta + \cos^2 \theta = 1$:
= $\frac{1 + \sin \theta \cos \theta}{\sin \theta \cos \theta}$
Splitting the fraction:
= $\frac{1}{\sin \theta \cos \theta} + \frac{\sin \theta \cos \theta}{\sin \theta \cos \theta}$
= $\text{cosec } \theta \sec \theta + 1$ = RHS
Hence Proved.
(iv) $\frac{1 \;+\; sec \;A}{sec \;A}$ = $\frac{sin^2 \;A}{1 \;-\; cos \;A}$
Proof
Simplifying LHS:
LHS = $\frac{1 + \sec A}{\sec A} = \frac{1 + \frac{1}{\cos A}}{\frac{1}{\cos A}} = \frac{\frac{\cos A + 1}{\cos A}}{\frac{1}{\cos A}} = \cos A + 1$
Simplifying RHS:
RHS = $\frac{\sin^2 A}{1 - \cos A} = \frac{1 - \cos^2 A}{1 - \cos A} = \frac{(1 - \cos A)(1 + \cos A)}{1 - \cos A} = 1 + \cos A$
Since LHS = RHS, the identity is proved.
(v) $\frac{cos \;A \;-\; sin \;A \;+\; 1}{cos \;A \;+\; sin \;A \;-\; 1}$ = cosec A + cot A
Proof
LHS = $\frac{\cos A - \sin A + 1}{\cos A + \sin A - 1}$
Divide the numerator and denominator by $\sin A$:
= $\frac{\frac{\cos A}{\sin A} - \frac{\sin A}{\sin A} + \frac{1}{\sin A}}{\frac{\cos A}{\sin A} + \frac{\sin A}{\sin A} - \frac{1}{\sin A}} = \frac{\cot A - 1 + \text{cosec } A}{\cot A + 1 - \text{cosec } A}$
Rearranging the terms:
= $\frac{(\cot A + \text{cosec } A) - 1}{(\cot A - \text{cosec } A) + 1}$
Using the identity $1 = \text{cosec}^2 A - \cot^2 A$ in the numerator:
= $\frac{(\cot A + \text{cosec } A) - (\text{cosec}^2 A - \cot^2 A)}{(\cot A - \text{cosec } A) + 1}$
= $\frac{(\cot A + \text{cosec } A) - (\text{cosec } A - \cot A)(\text{cosec } A + \cot A)}{\cot A - \text{cosec } A + 1}$
Taking $(\text{cosec } A + \cot A)$ common in the numerator:
= $\frac{(\text{cosec } A + \cot A) [1 - (\text{cosec } A - \cot A)]}{\cot A - \text{cosec } A + 1}$
= $\frac{(\text{cosec } A + \cot A) [1 - \text{cosec } A + \cot A]}{1 - \text{cosec } A + \cot A}$
= $\text{cosec } A + \cot A$ = RHS
Hence Proved.
(vi) $\sqrt{\frac{1 \;+\; sin \;A}{1 \;-\; sin \;A}}$ = sec A + tan A
Proof
LHS = $\sqrt{\frac{1 + \sin A}{1 - \sin A}}$
Multiply the numerator and denominator by $(1 + \sin A)$ inside the square root:
= $\sqrt{\frac{(1 + \sin A)(1 + \sin A)}{(1 - \sin A)(1 + \sin A)}} = \sqrt{\frac{(1 + \sin A)^2}{1 - \sin^2 A}}$
Using the identity $1 - \sin^2 A = \cos^2 A$:
= $\sqrt{\frac{(1 + \sin A)^2}{\cos^2 A}}$
= $\frac{1 + \sin A}{\cos A}$
Splitting the fraction:
= $\frac{1}{\cos A} + \frac{\sin A}{\cos A} = \sec A + \tan A$ = RHS
Hence Proved.
(vii) $\frac{sin \;θ \;-\; 2sin^3 \;θ}{2 cos^3 \;θ \;-\; cos \;θ}$ = tan θ
Proof
LHS = $\frac{\sin \theta - 2\sin^3 \theta}{2\cos^3 \theta - \cos \theta}$
Taking common factors from numerator and denominator:
= $\frac{\sin \theta (1 - 2\sin^2 \theta)}{\cos \theta (2\cos^2 \theta - 1)}$
= $\tan \theta \frac{1 - 2\sin^2 \theta}{2\cos^2 \theta - 1}$
Using the identity $\sin^2 \theta = 1 - \cos^2 \theta$ in the numerator:
= $\tan \theta \frac{1 - 2(1 - \cos^2 \theta)}{2\cos^2 \theta - 1}$
= $\tan \theta \frac{1 - 2 + 2\cos^2 \theta}{2\cos^2 \theta - 1}$
= $\tan \theta \frac{2\cos^2 \theta - 1}{2\cos^2 \theta - 1}$
= $\tan \theta \times 1 = \tan \theta$ = RHS
Hence Proved.
(viii) (sin A + cosec A)2 + (cos A + sec A)2 = 7 + tan2 A + cot2 A
Proof
LHS = $(\sin A + \text{cosec } A)^2 + (\cos A + \sec A)^2$
Expanding the squares:
= $(\sin^2 A + 2\sin A \text{cosec } A + \text{cosec}^2 A) + (\cos^2 A + 2\cos A \sec A \ $$ + \sec^2 A)$
Using reciprocal identities $\sin A \text{cosec } A = 1$ and $\cos A \sec A = 1$:
= $(\sin^2 A + 2 + \text{cosec}^2 A) + (\cos^2 A + 2 + \sec^2 A)$
Grouping terms:
= $(\sin^2 A + \cos^2 A) + 4 + \text{cosec}^2 A + \sec^2 A$
Using Pythagorean identities $\sin^2 A + \cos^2 A = 1$, $\text{cosec}^2 A = 1 + \cot^2 A$, $\sec^2 A = 1 + \tan^2 A$:
= $1 + 4 + (1 + \cot^2 A) + (1 + \tan^2 A)$
= $7 + \tan^2 A + \cot^2 A$ = RHS
Hence Proved.
(ix) (cosec A – sin A)(sec A – cos A) = $\frac{1}{tan \;A \;+\; cot \;A}$
Proof
Simplifying LHS:
LHS = $(\frac{1}{\sin A} - \sin A)(\frac{1}{\cos A} - \cos A)$
= $\left(\frac{1 - \sin^2 A}{\sin A}\right) \left(\frac{1 - \cos^2 A}{\cos A}\right)$
= $\left(\frac{\cos^2 A}{\sin A}\right) \left(\frac{\sin^2 A}{\cos A}\right) = \sin A \cos A$
Simplifying RHS:
RHS = $\frac{1}{\tan A + \cot A} = \frac{1}{\frac{\sin A}{\cos A} + \frac{\cos A}{\sin A}}$
= $\frac{1}{\frac{\sin^2 A + \cos^2 A}{\sin A \cos A}} = \frac{1}{\frac{1}{\sin A \cos A}} = \sin A \cos A$
Since LHS = RHS, the identity is proved.
(x) $\left( \frac{1\;+\;tan^{2}\;A}{1\;+\;cot^{2}\;A} \right)$ = $\left(\frac{1\;-\;tan \;A}{1\;-\;cot \;A} \right)^{2}$ = tan2 A
Proof
First, we prove $\frac{1 + \tan^2 A}{1 + \cot^2 A} = \tan^2 A$:
LHS = $\frac{1 + \tan^2 A}{1 + \cot^2 A} = \frac{\sec^2 A}{\text{cosec}^2 A} = \frac{1/\cos^2 A}{1/\sin^2 A} = \frac{\sin^2 A}{\cos^2 A} = \tan^2 A$
Next, we prove $\left(\frac{1 - \tan A}{1 - \cot A}\right)^2 = \tan^2 A$:
LHS = $\left(\frac{1 - \tan A}{1 - \frac{1}{\tan A}}\right)^2 = \left(\frac{1 - \tan A}{\frac{\tan A - 1}{\tan A}}\right)^2$
= $\left((1 - \tan A) \times \frac{\tan A}{\tan A - 1}\right)^2$
= $\left((1 - \tan A) \times \frac{\tan A}{-(1 - \tan A)}\right)^2$
= $(-\tan A)^2 = \tan^2 A$
Since both expressions simplify to $\tan^2 A$, the complete identity is proved.

